home  | más de cinemática | otros temas de Física | lecciones del maestro Ciruela | tonterías |  @ 
NO ME SALEN
EJERCICIOS RESUELTOS DE FÍSICA DEL CBC
(Movimiento uniformemente variado)
NMS c3.55 - Un proyectil es lanzado desde tierra, verticalmente hacia arriba, con velocidad inicial vo. Si el efecto del aire es insignificante, se cumple que:
a) el tiempo que tarda en caer al suelo es 4vo/g;
b) la distancia total recorrida por el proyectil es vo²/g;
c) si se duplica vo se duplica la altura máxima alcanzada;
d) la aceleración del proyectil cambia cuando comienza a bajar;
e) el proyectil llega a tierra con una velocidad menor que vo;
f) el proyectil llega a tierra con una velocidad mayor que vo.
  manolito

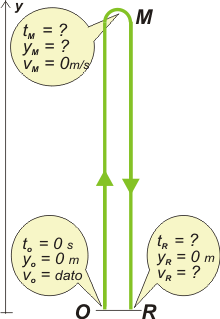
Odio este ejercicio. El motivo de mi odio es que genera que los estudiantes se pongan a coleccionar fórmulas: fórmula de la altura máxima, fórmula para tiempo de vuelo, fórmula para... ¡Y esas fórmulas no hacen falta, son basura! La cinemática (y todos los movimientos que te presentamos para que resuelvas algo) son sólo una excusa para que aprendas a usar las ecuaciones horarias.

OK, te lo hago... pero con la condición de que no tomes estos resultados para usarlos de fórmula rápida para calcular... lo que sea. Bueno, mirá el esquema:

    
Cinemática - No me salen - Ricardo Cabrera

Le puse nombre a los eventos en los que hay preguntas de enunciado: la llegada al punto más alto, M, y el regreso al punto de partida R.

Las ecuaciones que describen el movimiento:

y = vo . t – ½ g . t²

v = vo – g . t

Ahora empezamos a responder las preguntas. En esas ecuaciones están todas las respuestas. Pidámosles que hablen del punto R.

0 m = vo . tR – ½ g . tR²

vR= vo – g . tR

De la primera despejamos tR y calculamos. Yo te ayudo.
   

Se trata de una "cuadrática reducida" (no tiene término independiente) y se resuelve sacando factor común tR, así:

0 m = tR . ( vo – ½ g . tR)

Eso vale 0 cuando tR vale 0 (ese resultado lo descartamos porque no tiene sentido), y cuando todo el paréntesis vale 0, o sea:

0 = vo – ½ g . tR

De ahí despejo tP, -ahora sí, el que nos interesa-.

½ g . tR = vo

   
             tR = 2 vo / g            a) FALSA
   
Si con ese valor de tiempo de llegada al piso vamos a la ecuación de velocidad, obtenemos que:    
             vR = – vo            e) y f) FALSAS
   

Los enunciados e) y f) están hablando del módulo de la velocidad inicial, o sea de la rapidez, ya que para asignar signos hace falta establecer SR, y el enunciado no se mete en ese asunto.

Vamos a ver qué pasa en el punto más alto.

yM = vo . tM – ½ g . tM²

0 m/s = vo – g . tM

de la segunda ecuación despejamos tM...

g . tM = vo

tM = vo / g

Ya lo sabíamos, porque el tiempo que tarda en alcanzar la altura máxima debe ser la mitad del que tarda en regresar al punto de partida. Bueno, con eso vamos a la primera ecuación:

yM = vo . (vo / g) – ½ g . (vo / g)²

yM = (vo² / g) – ½ (vo² / g)

yM = ½ (vo² / g)

yM = vo² /2 g

Y la distancia total recorrida, D, debe ser exactamente el doble de eso:

    
             D = vo² / g            b) VERDADERA
   

Ahora supongamos que el proyectil es lanzado con una velocidad inicial distinta (la voy a llamar vi) que es el doble de la anterior:

vi = 2 vo

Es obvio que va a llegar más alto... pero cuánto más alto. A esa nueva altura la voy a llamar yN. Para hallar voy a tener que hacer exactamente lo mismo que hice antes, de modo que el resultado ya sé cuánto va a dar:

yN = vi² /2 g

Ahora, reemplazando la velocidad inicial por su equivalente...

yN = (2 vo)² /2 g

yN = 4 vo² /2 g

    
             yN = 4 yM            c) FALSA
   
La proposición d) no merece que la respondamos. Vos ya sabés que el signo de la aceleración NO DEPENDE de lo que haga el móvil (no importa si esta subiendo o bajando) sino que depende del sistema de referencia, pura y exclusivamente del sistema de referencia. (Uy, me parece que al final la respondí).    
DESAFIO: ¿Cuánto tarda en recorrer la mitad de su recorrido de ascenso?   Ricardo Cabrera
Algunos derechos reservados. Se permite su reproducción citando la fuente. También está permitido imprimirlo, prestarlo, regalarlo, donarlo y algunas otras cosas más que terminan en arlo. Última actualización may-10. Buenos Aires, Argentina.