NO ME SALEN
PROBLEMAS RESUELTOS DE FÍSICA DEL CBC
(Movimiento uniformemente variado)
|
|

|
 |
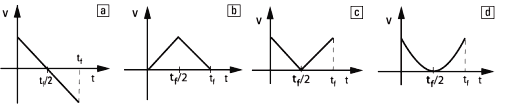
NS c3.54 - Indicar cuál de los siguientes gráficos
puede representar la velocidad en función del
tiempo de un cuerpo que en el instante 0 se arroja verticalmente
hacia arriba y regresa al punto de
partida. |
 |
|
Muy bonito ejercicio de gráficos. No te hacés suficiente idea de lo importante que es saber interpretar bien los gráficos y saber hacerlos a mano alzada, o sea cualitativamente. Vamos a ver si le sacamos provecho.
A cada gráfico que hagamos le voy a colocar en tandem su correspondiente de posición en función del tiempo. Eso nos va a servir para hacer la discusión. |
|
|
|
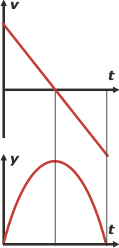
Espero que te hayas tomado un tiempo para hacer tu decisión. Porque el gráfico correcto es justamente éste, el a. Fijate cómo la velocidad cambia de signo, lo que habla a las claras de un movimiento de avance y retroceso.
Durante el avance la velocidad va disminuyendo (o sea: el móvil se va frenando) y en el retroceso el módulo de la velocidad va aumentando (o sea: el móvil regresa cada vez más rápido).
Fijate en el gráfico de posición-tiempo correspondiente al de velocidad. Se trata de una parábola de concavidad negativa (aceleración negativa), lo que se corresponde con una curva de velocidad descendente, que es justamente lo que tenemos.
Prestá atención a la inclinación de cada tramo de la parábola. Fijate que en el instante tf /2 no hay inclinación... y eso se corresponde con que la velocidad en ese mismo instante vale cero. |
|
| |
Como ves... hay muchas características que podés observar, discutir, chequear. Los lapsos de subida y bajada son iguales; las áreas que el gráfico de velocidad deja bajo la curva (un par de triángulos) también son iguales, lo que significa que el desplazamiento de subida es igual al de bajada... en fin... esto es infinito.
La gráfica de aceleración en función del tiempo correspondiente a estos gráficos sería una recta horizontal debajo del eje del tiempo (o sea: aceleración constante y negativa). |
|
|
|
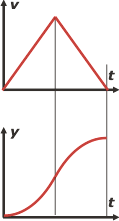
El gráfico b no puede describir un cuerpo que sube y baja. Podría describir un cuerpo que sólo sube o que sólo baja... porque la velocidad en todo el gráfico es positiva, es decir que la velocidad no cambia de sentido, lo que contradice el enunciado del ejercicio.
Mirá el gráfico de posición-tiempo correspondiente. Son dos arcos de parábola. El primer arco de concavidad positiva (velocidad creciente) y el segundo de concavidad negativa (velocidad decreciente).
Además se ve claramente cómo el móvil avanza permanentemente, nunca retrocede.
Prestale atención a las inclinaciones de las parábolas. Arranca y termina con inclinación nula (instantes en los que la gráfica de velocidad marca cero). Y su inclinación es mayor en el instante tf /2. |
|
|
|
| La gráfica de aceleración en función del tiempo correspondiente a estos gráficos sería un par de rectas horizontales la primera sobre el eje del tiempo y la segunda por debajo del eje del tiempo (o sea: dos aceleraciones constantes la primera positiva y la segunda negativa). |
|
|
|
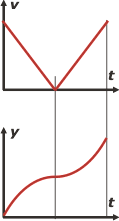
El gráfico c no puede describir un cuerpo que sube y baja. Podría describir un cuerpo que sólo sube o que sólo baja... porque la velocidad en todo el gráfico es positiva, es decir que la velocidad no cambia de sentido, lo que contradice el enunciado del ejercicio.
Mirá el gráfico de posición-tiempo correspondiente. Son dos arcos de parábola. El primer arco de concavidad negativa (velocidad decreciente) y el segundo de concavidad positiva (velocidad creciente).
Además se ve claramente cómo el móvil avanza permanentemente, nunca retrocede.
Prestale atención a las inclinaciones de las parábolas. Arranca y termina con inclinación máxima (instantes en los que la gráfica de velocidad marca valor máximo). Y su inclinación es nula en el instante tf /2. |
|
|
|
| La gráfica de aceleración en función del tiempo correspondiente a estos gráficos sería un par de rectas horizontales la primera debajo el eje del tiempo y la segunda por sobre el eje del tiempo (o sea: dos aceleraciones constantes la primera negativa y la segunda positiva). |
|
|
|
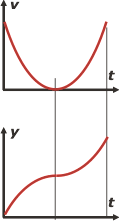
:El gráfico d no puede describir un cuerpo que sube y baja. Podría describir un cuerpo que sólo sube o que sólo baja... porque la velocidad en todo el gráfico es positiva, es decir que la velocidad no cambia de sentido, lo que contradice el enunciado del ejercicio.
Mirá el gráfico de posición-tiempo correspondiente. Son dos arcos de cúbica (muy difícil de distinguir a ojos vista de una parábola). El primer arco de concavidad negativa (velocidad decreciente) y el segundo de concavidad positiva (velocidad creciente).
Además se ve claramente cómo el móvil avanza permanentemente, nunca retrocede.
Prestale atención a las inclinaciones de las cúbicas. Arranca y termina con inclinación máxima (instantes en los que la gráfica de velocidad marca valor máximo). Y su inclinación es nula en el instante tf /2. |
|
|
|
La gráfica de aceleración en función del tiempo correspondiente a estos gráficos sería una recta oblicua creciente que intersecta al eje temporal en tf /2. |
|
|
| DESAFIO: ¿Con qué otro gráfico, además del a, se podría representar el movimiento descripto? |
|
 |
| Algunos derechos reservados.
Se permite su reproducción citando la fuente. Última actualización oct-13. Buenos Aires, Argentina. |
|
|
| |
| |
|

