NO ME SALEN
PROBLEMAS RESUELTOS DE FÍSICA DEL CBC
(Movimiento uniformemente variado)
|
|

|
 |
NMS c3.47 - Una piedra cae libremente, partiendo del
reposo. Hallar:
a - Su aceleración. (Justificar las hipótesis que
necesite).
b - El tiempo que tardará en alcanzar una velocidad
de 30 m/s.
c - La distancia recorrida en ese tiempo.
d - Su velocidad luego de recorrer 5 m.
e - El tiempo requerido para recorrer 500 m. |
|
Ya lo hice en otro ejercicio, pero voy a aprovechar éste para mostrar que las respuestas son independientes de la elección del sistema de referencia, y que el signo de la aceleración de la gravedad depende exclusivamente de este último.
En la columna de la izquierda, un SR positivo hacia arriba, y en el de la derecha, hacia abajo. Acá va el esquema doble.
| | |
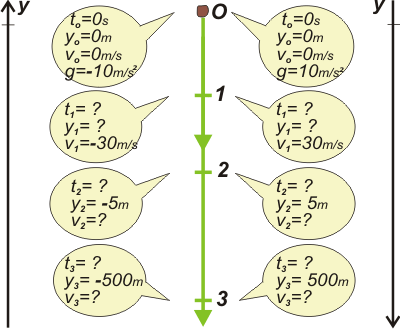 |
|
|
Los modelos de ecuación horaria de los movimientos libres verticales son éstos:
y = yo + vo ( t – to ) + ½ g ( t – to )²
v = vo + g ( t – to )
En ellos reemplazás las constantes iniciales (que te dibujé en azul). |
|
|
 |
|
 |
Las ecuaciones que describen TODA la caída son:
y = – 5 m/s² . t²
v = – 10 m/s² . t
A ellas les pedimos que hablen de los puntos en los que tenemos algún interés.
y1 = – 5 m/s² . t1²
– 30 m/s = – 10 m/s² . t1
Como noto tu ansiedad, te lo resuelvo:
t1 = – 30 m/s / – 10 m/s²
|
|
Las ecuaciones que describen TODA la caída son:
y = 5 m/s² . t²
v = 10 m/s² . t
A ellas les pedimos que hablen de los puntos en los que tenemos algún interés.
y1 = 5 m/s² . t1²
30 m/s = 10 m/s² . t1
Como noto tu ansiedad, te lo resuelvo:
t1 = 30 m/s / 10 m/s²
|
|
|
|
|
|
|
 |
|
 |
y1 = – 5 m/s² . 9 s²
y1 = – 45 m
|
|
y1 = 5 m/s² . 9 s²
y1 = 45 m
|
|
|
|
|
|
|
 |
|
 |
– 5 m = – 5 m/s² . t2²
v2 = – 10 m/s² . t2
|
|
5 m = 5 m/s² . t2²
v2 = 10 m/s² . t2
|
|
|
|
|
|
|
| |
v2 = – 10 m/s o v2 = 10 m/s |
|
|
|
|
 |
|
 |
Fijate que en esquema puse al instante 1 antes que al 2. Los números nos están desmintiendo. Pero no importa, el esquema nos sirvió igual. Vamos al 3.
– 500 m = – 5 m/s² . t3²
v3 = – 10 m/s² . t3
|
|
Fijate que en esquema puse al instante 1 antes que al 2. Los números nos están desmintiendo. Pero no importa, el esquema nos sirvió igual. Vamos al 3.
500 m = 5 m/s² . t3²
v3 = 10 m/s² . t3
|
|
|
|
| |
|
|
| |
v3 = – 100 m/s o v3 = 100 m/s |
|
|
|
|
| Te habrá quedado claro que el signo de las posiciones, de las velocidades y de la aceleración dependen del SR que hayamos elegido. Sin embargo, la interpretación física de los resultados es el mismo. Vamos con los gráficos. |
|
|
 |
|
 |
|
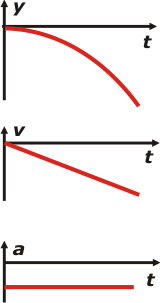
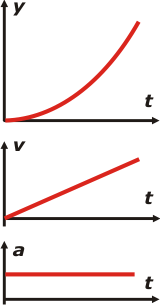
Como siempre en tándem, o sea, encolumnados en el orden preciso: posición-velocidad-aceleración.
Si quisieras consignar alguno de los valores que averiguamos en el ejercicio no te tenés que olvidar de colocar la unidad (entre paréntesis) y utilizar la misma escala de tiempo en los tres gráficos.
Quizás, lo que más le cuesta entender a los iniciados es que en los gráficos SIEMPRE se representan las variables crecientes hacia arriba y hacia la derecha. |
|
|
|
|
| Tal vez te haya llamado la atención una frase del enunciado: "Justificar las hipótesis que
necesite". Supongo que el autor se refería a que la aceleración vale g debido a que no hay ninguna fuerza frenando ni empujando ni desviando a la piedra durante su caída, que no sea su propio peso... por ejemplo, un rozamiento con el aire. Tal justificación es innecesaria ya que eso es justamente la definición de caída libre que anticipa el mismo enunciado. |
|
|
|
|
 |
| Desafío: No sólo el sentido del SR es una arbitrariedad que estemos facultados a elegir cada vez que resolvemos un ejercicio. Dónde colocamos los ceros, también. Resolvé nuevamente el ejercicio colocando los ceros de tiempos y posiciones en otro lugar. |
|
 |
|
| Algunos derechos reservados.
Se permite su reproducción citando la fuente. Última actualización jul-11. Buenos Aires, Argentina. |
|
|
| |
| |
|

