CINEMATICA, MRUV Ej 02, practica online de fisica

home

más de cinemática

otros temas de Física

lecciones del maestro Ciruela

tonterías

NO ME SALEN
PROBLEMAS RESUELTOS DE FÍSICA
(Movimiento uniformemente variado)

	NMS c3.35 - Los gráficos siguientes representan la velocidad que adquiere una bolita, en función del tiempo, al moverse en un camino rectilíneo (no necesariamente horizontal). (En esta página el gráfico 3) (Y en esta otra: gráfico 2)

Para cada uno de ellos se pide: a - Determinar su aceleración, y graficar a(t). b - Qué representa el área bajo la gráfica velocidad- tiempo, en el intervalo (2 s; 5 s). c - Escribir las ecuaciones horarias correspondientes, suponiendo que en t = 0 es x = 0. d - Hallar las posiciones correspondientes a los instantes t = 1 s; 4 s; 5 s; 7 s. Representarlas en un diagrama x(t) y trazar el gráfico orrespondiente. e - ¿Cuál es la pendiente de la recta tangente al gráfico x(t) en el punto correspondiente a t = 1 s, y por qué? f - ¿Qué representa el área bajo el gráfico aceleración-tiempo, en el intervalo (2 s; 5 s)? g – Describa, en cada caso, cómo vería moverse a la bolita

Acá hago el 3 a pedido de las masas. Supongo que te diste cuenta de que el gráfico del movimiento 1 representa un MRU. Vamos a lo nuestro:

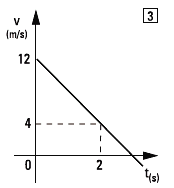
Primero hacé un esfuerzo de interpretación del gráfico. La velocidad no es la misma en todo instante. Está variando. Va disminuyendo a medida que corre el tiempo. Y disminuye uniformemente, por eso la gráfica es una recta descendente. Toda esa información me está diciendo que el gráfico describe un movimiento uniformemente variado (MRUV), y para hallar su aceleración constante podemos utilizar la definición de aceleración media:

a_m = ( v₂ – v₁) / ( t₂ – t₁)

Te habrás dado cuenta de que no usé los populares 0 y F (inicial y final) como subíndices en la definición. Es mucho más saludable hacer como hice yo. Darles dos nombres cualesquiera a dos instantes cualesquiera. (Usar inicial y final lleva a confusiones y errores).

Acá volqué en una tabla de valores los datos precisos que nos ofrece el gráfico (ofrece muchos más, infinitos, pero sólo esos cuatro en forma precisa).

v (m/s)	t (s)
12	0
4	2

O sea: dos pares de correspondencia entre v y t. No necesitás que sean inicial de nada ni final de nada. Dos pares cualesquiera. Eso es todo lo que necesitamos para hallar la aceleración:

en el MRUV la aceleración media coincide con la aceleración real del movimiento

a =		4 m/s – 12 m/s

		2 s – 0 s

a =		– 8 m/s

		2 s

a = – 4 m/s²

El gráfico lo voy a hacer al final porque lo que corresponde -para todo movimiento- es hacer todos los gráficos juntos, encolumnados y ordenados. Abajo te lo explico.

En todo gráfico v-t el área encerrada bajo la curva representa el desplazamiento del móvil en ese intervalo. El gráfico que nos muestra el enunciado no llega hasta los 5 s, pero vos podés continuarlo y luego calcular las áreas encerradas. Se trata de dos triángulos, uno sobre el eje de los tiempos y el otro debajo del eje. El área superior representa un avance y la inferior un retroceso. El desplazamiento buscado será la diferencia entre ambas áreas. En los gráficos de abajo la tenés sombreada.

área: ΔX_2s-5s

Ahora viene la parte más substanciosa del ejercicio: armar las ecuaciones horarias. (Es lo que tenés que hacer en todos y cada uno de los ejercicios de cinemática). Tenés que tener los modelos correspondientes (MRUV).

x = x_o + v_o ( t – t_o ) + ½ a ( t – t_o )²v = v_o + a ( t – t_o )

Y en esos modelos reemplazamos las constantes (que destaqué en azul) por una cuaterna de constantes del movimiento que se correspondan entre sí. Las únicas que nos brinda el enunciado son las que se corresponden con el instante t = 0 s. Que son: t_o = 0 s, x_o = 0 m, v_o = 12 m/s y a = – 4m/s². Reemplazamos, y las ecuaciones quedan así:

x = 0 m + 12 m/s ( t – 0 s) + ½ (– 4 m/s²)( t – 0 s)²v = 12 m/s + (– 4 m/s²)( t – 0 s)

O, más resumidamente, así:

x = 12 m/s t – 2 m/s² t²v = 12 m/s – 4 m/s² t

Una vez que armaste las ecuaciones, el movimiento no tiene más secretos para vos. Vamos a preguntarle cuáles son las posiciones en los instantes t_A= 1 s, t_B= 4 s, t_C= 5 s y t_D= 7 s.

en A	x_A = 12 m/s 1 s – 2 m/s² 1 s²
en B	x_B = 12 m/s 4 s – 2 m/s² 16 s²
en C	x_C = 12 m/s 5 s – 2 m/s² 25 s²
en D	x_D = 12 m/s 7 s – 2 m/s² 49 s²

x_A = 10 m; x_B = 16 m; x_C = 10 m; x_D = – 14 m

Ya que estamos, calculemos las velocidades correspondientes a esos instantes:

en A	v_A = 12 m/s – 4 m/s² 1 s
en B	v_B = 12 m/s – 4 m/s² 4 s
en C	v_C = 12 m/s – 4 m/s² 5 s
en D	v_D = 12 m/s – 4 m/s² 7 s

v_A = 8 m/s; v_B = – 4 m/s; v_C = – 8m/s; v_D = – 16 m/s

Bueno, ahora sí, le llegó el turno a los gráficos.

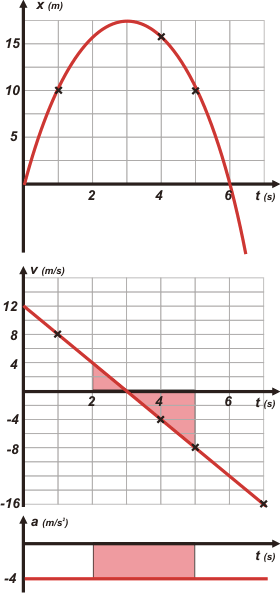
Mirá bien el orden en el que los encolumné: posición, velocidad, aceleración. No es arbitrario, tiene su lógica. Además están construídos con una misma escala de tiempo: fijate cómo las rayas verticales hacen coincidir los instantes en los 3 gráficos. A esta configuración le puse en nombre de tándem.

En el gráfico de posición te marqué tres de los cuatro puntos que calculamos arriba (el último me quedó un pofo fuera de escala). Esta vez no queda duda de que se trata de una parábola.

El área sombrada bajo la curva v-t entre 2 y 5 segundos equivale a... –6 m. Eso es exactamente lo que retrocede la bolita entre esos dos instantes. Verificá con las ecuaciones: x_2s= 16 m, x_5s= 10 m, Δx_2s-5s= –6 m.

El área sombrada bajo la curva a-t equivale al cambio de velocidad en ese intervalo. Disminuye de 4 a –8 metros por segundo, de modo que ese área debe medir Δv_2s-5s= –12 m/s. Se trata de un rectángulo cuya altura vale –4, y la base vale 3 (va desde el 2 hasta el 5).

Las áreas bajo la curva en los gráficos a-t no tienen mucho interés, en cambio en los gráficos v-t, sí.

Si adoptás la configuración tándem, después, no vas a aceptar ni permitir otra cosa.

fijate que la parábola ya arranca
(en 0s) con una inclinación hacia arriba.

DESAFIO: Hacer lo mismo para el caso 4 (te prometo que yo no lo voy a hacer).