CINEMATICA, No me salen 59, practica online de fisica

home

más de cinemática

otros temas de Física

lecciones del maestro Ciruela

tonterías

NO ME SALEN
PROBLEMAS RESUELTOS DE FÍSICA
(Movimientos libres verticales, encuentro)

manolito

*NMS c3.30 - El gráfico corresponde a dos móviles que se desplazan sobre la misma recta. Sabiendo que en t=0 B marcha delante de A a una distancia D, se cumple que:**
a) La distancia que separa los móviles varía cuadráticamente con el tiempo. b) El módulo de la aceleración de A es mayor que el módulo de la aceleración de B. c) Los móviles no se encuentran para t>0. d) Se produce un solo encuentro para t=D/8 (m/s). e) Se producen dos encuentros para t>0. f) La distancia que los separa crece linealmente con el tiempo.

*Este ejercicio fue tomado en el examen final de Física de julio de 2011.
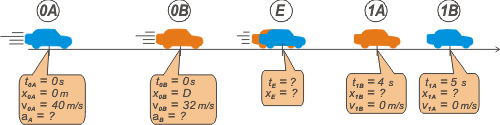
Para ver el tema de examen completo hacer click acá.

Ni se te ocurra empezar a resolver este ejercicio sin confeccionar un esquema.

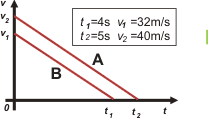
Ahí volqué todos los datos del gráfico y del enunciado, y agregué un hipotético encuentro. Armemos las ecuaciones:

móvil A → x_A = 40 m/s . t + ½ a_A . t²

v_A = 40 m/s + a_A . t

móvil B → x_B = D + 32 m/s . t + ½ a_B . t²

v_B = 32 m/s + a_B . t

Pidámosle a las ecuaciones de velocidad que hablen de los momentos en los que la velocidad se anula.

0 m/s = 40 m/s + a_A . 5 s

0 m/s = 32 m/s + a_B . 4 s

Si las resolvés vas a encontrar que la aceleración de ambos móviles vale lo mismo:

a_A = a_B = — 8 m/s²

Cosa que seguramente ya habías anticipado porque la gráfica de velocidades nos muestra dos rectas oblicuas descendentes y paralelas. Bueno, con esto podemos empezar a contestar las opciones del ejercicio.

a) La distancia que separa los móviles varía cuadráticamente con el tiempo. FALSO, la distancia entre los móviles no es otra cosa que la resta entre las ecuaciones de posición.

x_A — x_B = 40 m/s . t — 4 m/s² . t² — (D + 32 m/s . t — 4 m/s². t²)

x_A — x_B = 40 m/s . t — 4 m/s² . t² — D — 32 m/s . t + 4 m/s². t²

x_A — x_B = 8 m/s . t — D

La distancia varía linalmente, no en forma cuadrática.

b) El módulo de la aceleración de A es mayor que el módulo de la aceleración de B. FALSO, ya está dicho y calculado.

c) Los móviles no se encuentran para t>0. FALSO. Resolvamos el encuentro a ver qué pasa.

40 m/s . t_E — 4 m/s² . t_E² = D + 32 m/s . t_E — 4 m/s². t_E²

8 m/s . t_E = D

t_E = D / 8 m/s

d) Se produce un solo encuentro para t=D/8 (m/s). VERDADERO. (Salvo por que sobran los paréntesis que envuelven a las unidades).

e) Se producen dos encuentros para t>0. FALSO. La respuesta que encontramos para el encuentro era única. Luego, es un solo encuentro.

f) La distancia que los separa crece linealmente con el tiempo. FALSO. La distancia decrece con el tiempo.

Se produce un solo encuentro
para t = D/8 (m/s)

opción d)

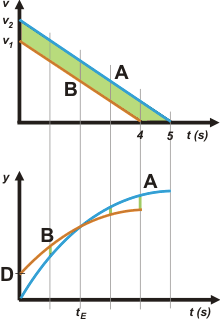
También es cierto que todo (o casi todo) se podía contestar con sólo mirar el gráfico. Para analizar esta variante tan interesante te vuelvo a presentar el gráfico del enunciado y lo acompaño, abajo, del gráfico correspondiente de posiciones.

Cinemática - No me salen - Ricardo Cabrera

La distancia entre los móviles está representada por el rectángulo que te sombreé en verde, que no es otra cosa que la resta entre el desplazamiento del móvil A menos el desplazamiento del móvil B (acordate que el desplazamiento está representado por el área encerrada bajo la curva v-t). A medida que trancurre el tiempo el área del rectángulo crece linealmente (en una sola dimensión).

Lo de las aceleraciones ya lo dijimos, se ve en el paralelismo de las curvas v-t.

El asunto del encuentro es más sutil. Que haya o no haya encuentro, en realidad, depende del valor de D. Pero como las parábolas que representan las posiciones son idénticas (igual aceleración) puede haber uno y sólo un encuentro.

La barritas verdes representan la distancia entre los móviles.

Bueno, me cansé.

DESAFIO: ¿Cuánto debe valer, como mínimo, D para que los móviles se encuentren antes de detenerse?