home  | más de cinemática | otros temas de Física | lecciones del maestro Ciruela | tonterías |  @ 
NO ME SALEN
EJERCICIOS RESUELTOS DE FÍSICA
(Movimiento rectilíneo uniformemente variado)

 

manolito

NMS c3.27 - Un auto viaja a 16,67 m/s a lo largo de una pista recta. El conductor del auto ve un camión que viaja delante él a una distancia de 5 m y con una velocidad de 40 km/h. El conductor del auto aplica los frenos a los 0,5 s de haber observado el camión, generando una aceleración de 50 cm/s².

    a) Haga un diagrama ilustrativo de la situación planteada, incluyendo el sistema de referencia a emplear.
    b) Plantee las ecuaciones cinemáticas de posición y velocidad que rigen el movimiento del auto y del camión.
    c) ¿El auto alcanza al camión?

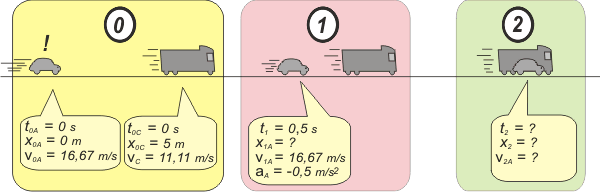
¡Qué terrible! Un ejercicio con dos móviles de los cuales uno, encima, me cambia de movimiento... ¡¡¡me quiero suicidar!!!

El enunciado lo llama diagrama ilustrativo, pero es el esquema. (Qué creativa que es la gente).

    

A ver si estás de acuerdo. Llamé 0 al instante inicial, verificá los valores que puse porque son los que vamos a usar para armar las ecuaciones horarias de los móviles. Pasé las velocidades a unidades internacionales para unificarlas con el resto de los datos.

40 km/h = 11,11 m/s;    50 cm/s² = 0,5 m/s²

Al instante en el que el auto cambia el tipo de marcha lo llamé 1, que, según dice el enunciado es 0,5 segundos después de 0. No me interesa dónde anda el camión en ese momento, por eso no le puse indicaciones.

Y el instante en se encuentran (supuestamente) lo llamé 2. Las ecuaciones nos dirán si ese encuentro se produjo o si no se produjo.

Con la ayuda del esquema, armar las ecuaciones es un juego de niños.

   si no te acordás cómo se hacen los pasajes de unidades podés ir a refrescar la memoria acá
auto entre 0 y 1 x = 16,67 m/s . t  
camión

x = 5 m + 11,11 m/s . t

  
auto entre 1 y 2 x = x1A + 16,67 m/s (t — 0,5 s) — 0,25 m/s² (t — 0,5 s)²  
auto entre 1 y 2 v = 16,67 m/s — 0,5 m/s² (t — 0,5 s)  
  PASO DOS
ARMAR
LAS ECUACIONES
Ahora les vamos a pedir a esas ecuaciones que hablen de los instantes en los que tenemos interés (el instante 1 sólo para el auto y el instante 2 para ambos).    
auto en 1 x1A = 16,67 m/s . 0,5 s [1]
camión en 2

x2 = 5 m + 11,11 m/s . t2

 [2]
auto en 2 x2 = x1A + 16,67 m/s (t2 — 0,5 s) — 0,25 m/s² (t2 — 0,5 s)² [3]
auto en 2 v2A = 16,67 m/s — 0,5 m/s² (t2 — 0,5 s) [4]
  PASO TRES
USAR
LAS ECUACIONES

Y como siempre... desembocamos en un sistema de ecuaciones con tantas ecuaciones como incógnitas... ¡aleluya, hermano!, ¡aleluya!... hemos resuelto el ejercicio... por lo menos la física del ejercicio, que era lo que nos interesaba. El resto es álgebra (salvo las interpretaciones finales que faltan).

Resolvamos por este camino (que no es el único). De la ecuación [1] calculamos la posición del auto cuando cambia de movimiento.

x1A = 8,34 m

Con ese valor vamos a la ecuación [3] que igualamos a la [2].

  

PASO CUATRO
CONTAR
LAS ECUACIONES Y LAS INCÓGNITAS

 

PASO CINCO
RESOLVER
          5 m + 11,11 m/s . t2 = 8,34 m + 16,67 m/s (t2 — 0,5s) — 0,25 m/s² (t2 — 0,5s)²

¡Uf! ¡Qué largo! Bueno... no protestes que lo estoy haciendo yo. Pero no estaría mal que vos lo intentes sin ayuda. Finalmente tenés que llegar a una expresión como ésta:

0 = — 5,06 m + 5,81 m/s . t2 — 0,25 m/s² . t2²

O sea, una ecuación cuadrática cuya solución (si es que la tiene) encontraremos de esta manera:

    
            te cuento que lo que está dentro de la raíz se llama discriminante
Y que arroja dos resultados: t2 = 0,9 s y t2b = 22,3 s. Obviamente el que nos interesa es el primer encuentro (cuando al auto alcanza al camión), de modo que:    
 

           t2 = 0,9 s

  
   

Nos fijamos tanto en la ecuación [2] como en la [3] (verificando que nos de el mismo resultado) que la posición de encuentro es:

   
 

           x2 = 15 m

  
   

Aprovecho este momento para mostrarte los gráficos y dicutirlos un poco.

Los hice fuera de escala por motivos obvios, pero están bastante correctos en lo cualitativo.

El auto en verde (primera parte verde claro y segunda parte verde oscuro), y el camión en rojo.

Fijate que la parábola (verde oscuro) que representa la frenada del auto podría haber sido más cerrada y no tocar la línea roja o no tan cerrada y tocarla solo una vez.

Las tres posibilidades aparecían en nuestra resolución (el discriminante de la cuadrática): dos resultados, o uno (si el discriminante vale cero) o ninguno (si el discriminante es negativo ya que no existe la raíz cuadrada de un número negativo).
  PASO SEIS
GRÁFICOS

Aunque el enunciado no lo pregunta, podríamos averiguar la velocidad que tiene el auto en cada cruce y verificar que en t2 todavía tiene una velocidad superior a la del camión (si no no podría pasarlo) y en t2b tiene una velocidad inferior (si no el camión no podría volver a cruzarlo). Es hora de usar la ecuación [4].

v2A = 16,67 m/s — 0,5 m/s² ( 0,9 s — 0,5 s)

v2bA = 16,67 m/s — 0,5 m/s² ( 22,3 s — 0,5 s)

Efectivamente, v2A = 16,47 m/s y v2bA = 5,57 m/s.

    
     

DESAFIO: ¿En qué instante el auto tiene la misma velocidad que el camión?

  Ricardo Cabrera
Algunos derechos reservados. Prohibida su impresión en impresoras berretas. Se permite su reproducción citando la fuente. Última actualización abr-13. Buenos Aires, Argentina.