 |
NO ME SALEN
PROBLEMAS RESUELTOS DE FÍSICA DEL CBC
(MRUV, tiro vertical, caída libre)

|
|

|
NMS c3.13 - Una estudiante lanza un llavero hacia arriba, a su hermana, que está en una ventana 5 m más arriba. Las llaves son detenidas por el brazo extendido de su hermana, pero no puede atraparlas, cayendo a manos de la estudiante que las arrojó, quien las recibe 1,6 s después de que las lanzó. (Considere despreciable el tiempo necesario para detener las llaves).
a) ¿Con qué velocidad inicial fueron lanzadas las llaves?
b) ¿Cuál era la velocidad de las llaves justo antes de ser detenidas por la hermana de la estudiante?
Como siempre, empecemos con un esquema. |
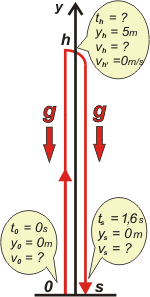 |
Pequeñas sutilezas del planteo que estoy seguro de que las resolvés correctamente, pero que no viene mal aclarar: es obvio que la llave no sale del piso, sino de la mano de la estudiante... el sentido del ejercicio radica en que la distancia entre la mano arrojadora y la receptora mide 5 metros.
Tampoco es inmediato entender lo que ocurre allá arriba. La intervención de la hermana sólo consiste en detener, frenar, el llavero. También podría pensarse que la llave pasa de largo y que la intervención de la hermana ocurre durante la bajada de las llaves... pero es más rebuscado. La cuestión es que cuando la hermana toca el llavero, inmediatamente sale hacia abajo desde el reposo. Fijate que en el esquema puse dos velocidades para ese instante: vh es la velocidad con la que el llavero llega a la mano de la hermana, y vh´, la velocidad con la que empieza a bajar... que vale cero. Mirá el esquema.
Por último, y como hago siempre, uso un único SR con una única escala de posición y una única escala de tiempo. Después voy a volver a hacer un comentario sobre ésto. |
|
|
|
Tenemos dos movimientos, ambos libres verticales: uno de ascenso y otro diferente de descenso. Tienen cosas en común (como que uno empieza justo cuando termina el otro, también que tienen la misma aceleración...), pero como son dos movimientos diferentes tienen que tener ecuaciones horarias diferentes; ambas del mismo tipo, y cuyos modelos son éstos: |
|
|
y = yo + vo ( t – to) + ½ g ( t – to)²
v = vo ( t – to) + g ( t – to)
|
modelos
(para cualquier MRUV vertical libre) |
De modo que el ejercicio debe describirse con cuatro ecuaciones: dos para el movimiento de ascenso y dos para el de descenso. Las cuatro se construyen de la misma manera: reemplazando las constantes de los modelos (to, yo, vo, y g) por las constantes iniciales de cada movimiento. Así quedan: |
|
| ascenso |
y = vo . t – 5 m/s² . t² |
| v = vo – 10 m/s² . t |
| descenso |
y = 5 m – 5 m/s² . ( t – th)² |
| v = – 10 m/s² . ( t – th)² |
|
ecuaciones
(que describen todo el movimiento narrado en el enunciado) |
| Ahora les pedimos a las cuatro ecuaciones que hablen de los eventos interesantes de los que pueden hablar cada una: las del ascenso pueden decir algo piola en el instante en que la hermana las detiene; y las del descenso pueden decir algo interesante cuando regresan a manos de la estudiante, o sea, en el instante 1,6 s. |
|
| ascenso en th |
5 m = vo . th – 5 m/s² . th² |
[1] |
| vh = vo – 10 m/s² . th |
[2] |
| descenso en F |
0 m = 5 m – 5 m/s² . ( 1,6 s – th)² |
[3] |
| vF = – 10 m/s² . ( 1,6 s – th) |
[4] |
|
ecuaciones especializadas
(sólo hablan de los momentos interesantes del movimiento) |
Y a dónde te creés que llegaste: a un sistema de tantas ecuaciones como incógnitas en donde las incógnitas son las que te pide el enunciado del ejercicio. No inventamos nada, no hicimos para este planteo nada que no hayamos hecho para todos los ejercicios de cinemática... El resto es álgebra. Es muy importante que visualices este límite entre la física y el álgebra. Si lo hacés... ya podés ir sintiéndote físico... porque te lo ganaste.
Te cuento cómo vamos a resolverlo: la ecuación [4] la vamos a ignorar, ya que no aporta información interesante ni el enunciado nos pide averiguar la velocidad con la que llega el llavero de regreso (aunque podría). El resto es un sistema de 3x3. De la última vamos a sacar el valor de th. Ojo, es una cuadrática que para ordenarla tenés que desarrollar el cuadrado del binomio. Acá va:
0 m = 5 m – 5 m/s² . [ (1,6 s)² – 2 . 1,6 s . th + th² ]
0 m = 5 m – 5 m/s² . [ 2,56 s² – 3,2 s . th + th² ]
0 m = 5 m – 12,8 m + 16 m/s . th – 5 m/s² . th²
0 m = – 7,8 m + 16 m/s . th – 5 m/s² . th²
Ahora sí se distinguen perfectamente los coeficientes cuadrático (a), lineal (b) e independiente (c) de la cuadrática: |
|
a = – 5 m/s² , b = 16 m/s y c = – 7,8 m
|
|
|
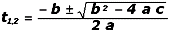
|
|
|
th = 0,6 s
Descartamos el otro valor, t'h = 2,6 s porque, claramente, no es el que buscamos. Ahora, sabiendo cuánto vale th, vamos a la ecuación [1] y despejamos vo...
5 m = vo . 0,6 s – 5 m/s² . 0,36 s²
|
|
|
|
|
|
Por último vamos a la ecuación [2] y despejamos vh
vh = 11,33 m/s – 10 m/s² . 0,6 s
|
|
|
|
|
|
Si nos hubiesen pedido el valor de la velocidad al recuperar el llavero, habríamos usado la ecuación [4] y habríamos obtenido vF = – 10 m/s. |
|
|
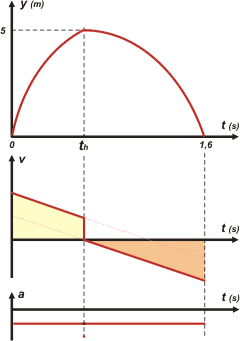 |
Los gráficos, como siempre en tándem, nos revelan detalles y propiedades del ejercicio que no es bueno pasar por alto.
Mirá las áreas sombreadas en el gráfico de velocidad: ambas deben valer 5 metros. La segunda es un triángulo, eso es muy fácil... y la primera, un trapecio. Chequealo. En ambos tramos, las curvas de variación son rectas; y ambas deben ser paralelas (te las prolongué para que pudieras apreciarlo) pues la aceleración es la misma en ambos casos, tal como se muestra en la gráfica de abajo.
El salto de velocidad que se da en la atajada de la hermana nos enfrenta a un compromiso: si respetamos las condiciones de nuestro universo deberíamos llenar el salto con un trazo (eso es lo que hice), pero el lenguaje de los gráficos lo prohíbe (sabrán disculparnos).
¿Captás el detalle en el gráfico de aceleración? ¿Hay conflicto con éste? |
|
|
|
Discusión: apostaría que tanto el 95% de los estudiantes que resolvieron este ejercicio correctamente, como el 80% de los profesores de física que lo resuelven frente a un curso como parte de la práctica, lo hacen de este modo: con la fórmula de caída libre h = ½gΔt averiguan el valor del intervalo de la caída (y les da 1 s). Eso se lo restan al tiempo total del viaje (que les da 0,6 s). Conociendo ese tiempo van a la fórmula de distancia de un MRUV, d = vo Δt – ½ g Δt², de donde despejan vo; finalmente, usan la expresión de aceleración, con la que obtienen el valor de la velocidad en la atajada a medias de la hermana.
Ok, llegan al mismo resultado... pero desarrollan una física formulerista*, alejada del concepto fundamental de la función real (en el caso de la cinemática: la ecuación horaria). Por otro lado... qué hay más sencillo para un físico que plantear toda la historia desde un único sistema de referencia. Ya sabemos lo que se pierde el planteo formulerista... pero ¿qué gana? ¿Sencillez algebraica? |
|
|
*Formulerista. Arrabal porteño. Dícese del estudiante que no manya un pomo de Física y trata de zafar aplicando fórmulas al tuntún que, por las letras que poseen, parecen encajar en el asunto que pretende descular. Proviene del castizo formulista.
1. adj. Dicho de una persona: Partidaria del formulismo.
formulismo.
1. m. Excesivo apego a las fórmulas en la resolución y ejecución de cualquier asunto, especialmente de los oficiales y burocráticos. |
|
 |
| DESAFIO: ¿Cuál de las áreas sombreadas en el gráfico velocidad-tiempo es mayor? ¿Por qué las pendientes de las rectas en ese gráfico son iguales? |
|
| |
|
| Algunos derechos reservados (en criollo: no podés publicarlo a tu nombre, ¿entendiste? Mirá que tengo un boga repesado, ¿eh?).
Eso sí, se permite su reproducción citando la fuente. Última actualización jun-08. Buenos Aires, Argentina. |
|
|
|

