 |
NO ME SALEN
EJERCICIOS RESUELTOS DE FÍSICA DEL CBC
(movimientos concatenados: uniforme y variado)
|
|

|
NMS c3.10*- Desde la boca de un pozo profundo se suelta una piedra que cae libremente. El ruido que produce al llegar al fondo se escucha exactamente 4,7 segundos después de haberla soltado. Sabiendo que el sonido viaja a una velocidad constante de 340 m/s, hallar la profundidad del pozo. |
Este problema es uno de los clásicos de la cinemática. Figura en todos los libros de Física menos en uno. Según el libro de los récords de Guinness fue tomado en 4.485.629 exámenes de Física de todo el mundo hasta el año 2001. Y sigue cosechando víctimas por doquier. No me salen no podía quedarse sin resolverlo. Eso sí... a nuestra manera. Primero el esquema. |
|
|
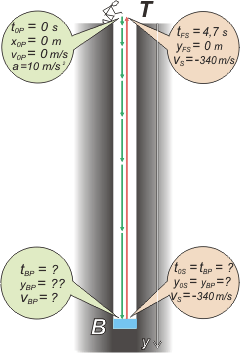 |
Dibujé la caída libre de la piedra en verde. Tomé un SR vertical que apunta hacia abajo (ojo, hay que usar el mismo SR para todo el problema, si no viene el cuco y te comerá). La piedra se queda abajo, pero inmediatamente sale hacia arriba la onda sonora que viaja con MRU. La dibujé en rojo.
Lo más importante de los esquemas son los datos (o incógnitas) que consignás en los globitos. Es recontra importante que les pongas nombres claros y valores correctos. Un error acá... y fuiste, nada te salva. El globito verde de arriba lo voy a usar para armar la ecuación horaria de la piedra, cuyo modelo es
y = yo + vo ( t – to ) + ½ g ( t – to )²
y el globito rosa de abajo para la ecuación del sonido, cuyo modelo es
y = yo + v ( t – to )
Es facilísimo. Reemplazo las constantes (lo que está en azul) haciendo CTRL+C y CTRL+V. Un juego de niños. |
|
|
| piedra |
|
y = 5 m/s² t ² |
|
| sonido |
|
y = yBP – 340 m/s ( t – tBP ) |
|
|
|
Ahora les pido a esas ecuaciones, que describen todo el movimiento de los dos móviles, que hablen exclusivamente de los sucesos que me interesan: la de la piedra va a hablar del fondo del pozo y la del sonido de la superficie, donde pongo la oreja. Fijate que cuando se usa una ecuación horaria, cuando se especializa para un suceso en particular... sólo se reemplazan las variables |
|
| piedra |
 |
yBP = 5 m/s2 tBP² |
habla de B (bottom) |
| sonido |
0 m = yBP – 340 m/s ( 4,7 s – tBP ) |
habla de T (top) |
|
|
Lo sospeché desde un principio: irremediablemente desembocamos en un sistema de dos ecuaciones con dos incógnitas... se acabó la Física, se viene el álgebra... que por suerte, esta vez, es bastante sencillita. Intentalo sin mi ayuda. Cualquier cosa volvé.
Volviste... en la ecuación del sonido reemplazo yBP por lo que indica la de la piedra:
0 m = 5 m/s2 . tBP² – 340 m/s ( 4,7 s – tBP )
0 m = 5 m/s2 . tBP² – 1.598 m + 340 m/s . tBP
te quedó una cuadrática común y silvestre, ya la tenés igualada a cero, y los coeficientes son A = 5 m/s², B = 340 m/s y C = – 1.598 m. Así obtenemos dos valores posibles para tBP; el nuestro es:
tBP = 4,413 s
con este valor vuelvo a la ecuación de la piedra y obtengo |
|
|
|
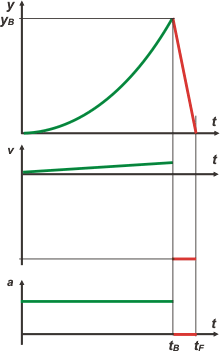
| O sea, con una soguita de 100 metros puedo tomar agua. Mirá los gráficos. |
|
 |
DESAFIO: Más fácil: decime la velocidad de la piedra al llegar al fondo. Más difícil: en la resolución de la cuadrática habrás descartado un valor de – 72,4 s para el instante del fondo (una locura)... pero... ¿te animás a buscarle una interpretación física? |
| |
| *Ejercicio tomado en el primer parcial de Física del año 1985, 86, 87, 88, 89, 90, 92, 93, 94, 95, 96, 98, 99, 2000, 02, 03, 04, 05 y 06, en alguna de las sedes del CBC. |
|
| |
| |
Algunos derechos reservados.
Se permite su reproducción citando la fuente. Última actualización abr-07. Buenos Aires, Argentina. |
|
 |
| |
| |
|
|

