home  | más de cinemática | otros temas de Física | lecciones del maestro Ciruela | tonterías |  @ 
NO ME SALEN
APUNTES Y EJERCICIOS RESUELTOS DE FÍSICA DEL CBC


  

manolito

NMS c3.05 - En una carrera de relevos, el competidor A que viene corriendo con velocidad constante vA debe entregar un bastón (testimonio) a su compañero de equipo, B, en un punto Q establecido de la pista. B espera en reposo en un punto P, a una distancia d antes de Q. Sabiendo que la entrega debe hacerse con ambos competidores a la par, corriendo a la misma velocidad, y suponiendo que B se desplaza con aceleración constante hasta el encuentro, determinar cuál debe ser la distancia entre ambos en el instante de arranque de B.

Mi tía Harriet siempre me decía: "cuando no entiendes un enunciado, y lo vuelves a leer y no lo entiendes, y luego lo vuelves a leer y sigues sin entenderlo... entonces es porque se trata del enunciado del problema cuatro de la serie de adicionales de la guía de Física del CBC". ¡Ay, tiíta! Cuánta razón tenías... y yo que no te hacía caso.

Pero tomémoslo con calma y, como hubiese hecho la tía, y pidámosles ayuda a unos "esquemas secuenciales disney".

    
Adriana viene corriendo a velocidad constante y cuando pasa por O, ahí justo, arranca Bernardo.
Mientras Bernardo acelera, Adriana sigue a velocidad constante. Ya está por alcanzarlo.
Justo quedan a la par al pasar por Q, y recién ahí Bernardo alcanza la velocidad de Adriana.
 
   
Ahora sí... ¡¿Pero qué quieren que calcule si en este problema no hay ni un solo dato?! Bueno, ya sé, lo que quieren que averigüemos es d', la distancia entre O y P. Es cierto que con esta falta de datos numéricos no podremos decir cuánto vale d', pero tal vez podamos decir cuánto vale en función de esos otros datos que nombraron, vA y d, y que no nos dijeron cuánto valían. (O sea, les vamos a pagar con la misma moneda). Alterando un poco el orden de siempre, te refuerzo las ideas de lo que ocurre en el ejercicio con unos gráficos.    

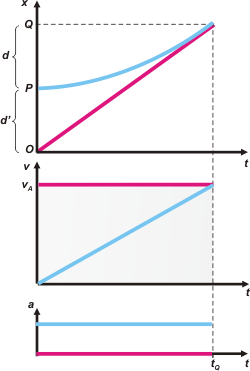
En los gráficos se ve bien el tipo de movimiento de cada uno: MRU para Adriana (rosa, lógicamente) y MRUV para Bernardo (celeste, como todo varoncito); también se ve que Bernardo arranca del reposo; que Adriana alcanza a Bernardo recién en Q; se ve la distancia que los separa cuando arranca Bernardo, d' (nuestra incógnita); y la distancia d que separa los puntos P y Q...

¡Alto! ¡Alto! ¡Ya resolví el problema! ¡Lo saqué, lo saqué! ¡Olé, olé, sachicha con puré! Mirá con atención el segundo gráfico. Recordemos que el área encerrada bajo la curva de un gráfico velocidad-tiempo representa el desplazamiento del móvil. Bien, para Bernardo es el área de un triángulo, y sabemos que su desplazamiento es d, y para Adriana es un rectángulo, y su desplazamiento es d'+ d... Pero el rectángulo es el doble que el triángulo, por lo tanto  d' = d. ¡Oso...!
   
Pero vamos a resolverlo por vía de las ecuaciones horarias, para demostrarle a la tía Harriet que ellas lo pueden todo. ¿Cuántas ecuaciones describen todo el problema? Tres, of course, dos para Bernardo, una para Adriana. Las ecuaciones las hallo como siempre: reemplazo las constantes (to, xo, vo y a) de los modelos que siempre tengo a mano...    
MRU x = xo + v ( t – to )
MRUV x = xo + vo ( t – to ) + ½ a ( t – to )²
v = vo + a ( t – to )
  Los modelos
...por las constantes que representan los movimientos del problema y que ya están consignadas, agrupaditas y ordenaditas en el esquema: para Adriana en el punto 0 y para Bernardo en el punto P. Si somos metódicos y no nos equivocamos, las ecuaciones quedan así:    
Adriana x = vA . t
Bernardo x = d' + ½ aB . t²
v = aB . t
  Estas son las ecuaciones que describen TODO el fenómeno del movimiento contado en el enunciado
Ahora las usamos (las "especializamos", como dicen los físicos); es decir, les pedimos que hablen del punto Q. Acordate que usar una ecuación horaria es reemplazar las variables. Tené presente que la posición de Q es (d´+ d), y que la velocidad de Bernardo en esa posición es igual a la de Adriana.    
d' + d = vA . tQ [1]
d' + d = d' + ½ aB . tQ² [2]
vA = aB . tQ [3]
  Estas son las ecuaciones que hablan solamente de los puntos que nos interesan, o sea: Q.

Por último operamos algebraicamente. La idea es obtener una expresión de d' en la que no aparezcan otras constantes que no sean los datos del problema, es decir, vA y d. Seguime, vas a ver que no es difícil.

En la ecuación [1], donde dice vA, reemplazo la [3]

d' + d = aB . tQ²                                                 [4]

en la ecuación [2] cancelo d' (fijate que está en los dos miembros), y multiplico toda la expresión por 2.

2 d = aB . tQ²                                                     [5]

ahora igualo [4] con [5] (fijate que el segundo miembro es el mismo para ambas).

d' + d = 2 d'

cancelo una de las d'

   
 

d' = d

(lo sabía)

   
O sea: si Bernardo está a 20 metros del límite para pasar la posta, tiene que arrancar cuando Adriana esté a 20 metros de él, o sea, a 40 del límite.    
DESAFIO: Mejorar la redacción del enunciado para que la tía Harriet no proteste (si resucita, la pobre).   Ricardo Cabrera
Prohibida la reproducción total o parcial de este material didáctico de primerísima calidad por cualquier medio visual, gráfico, sonoro o tridimensional de mala calidad. Las transgresiones a esta disposición serán penalizadas con 25 años de reclusión en la Antártida y trabajos forzosos. Sólo se permite su reproducción citando la fuente. Algunos derechos reservados. Última actualización ago-06. Buenos Aires, Argentina.