 |
NO ME SALEN
PROBLEMAS RESUELTOS DE FÍSICA DEL CBC
(Movimiento uniforme)
|
|

|
| NMS c2.16- Un calefón avanza por un camino recto y a velocidad constante de 1,5 m/s y entra por una ventana de la casa a las 15:30:00. 4 segundos después por la ventana opuesta entra una garrafa moviéndose también a velocidad constante de 2 m/s. Si se encuentran a los 5,45 segundos de haber ingresado el calefón, ¿cuál es la distancia que separa ambas ventanas? |
|
No puede ser... habría que prohibirles a los autores de ejercicios trabajar mientras están drogados. En fin, ya lo hizo. Resolvamos. Como siempre, empezamos con un esquema.
|
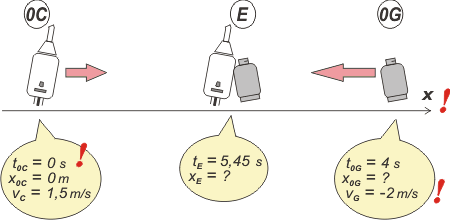 |
|
|
Acá lo tenés... prestá atención sobre todo a las cosas que le puse al lado un signo de admiración, se trata de decisiones arbitrarias: el sentido del SR, la posición y el instante iniciales del calefón... Y también los signos de la velocidades, que dependen de la decisión anterior sobre el sentido del SR.
¿Cuántas ecuaciones horarias describen este problema? Dos, ya que hay dos móviles. Ambas surgen del mismo modelo ya que ambos se mueven uniformemente. El modelo es este:
x = xo + v ( t – to )
Y, por lo tanto, reemplazo las constantes del modelo (azules) mirando las constantes elegidas en el esquema, de modo que las ecuaciones de este problema son: |
|
|
| |
la del calefón
la de la garrafa |
x = 1,5 m/s . t
x = xOG – 2 m/s . ( t – 4 s ) |
|
Estas son las ecuaciones que describen TODO el movimiento descripto en el enunciado. |
| Ahora, ellas solitas resuelven el problema. Pidámosles que en lugar de hablar de las infinitas posiciones y sus respectivos instantes de tiempo por los que pasan el calefón y la garrafa, se refieran exclusivamente a la posición e instante de encuentro. (Ahora es cuando reemplazo las variables, las rojas). Entonces dicen: |
|
|
| |
 |
xe = 1,5 m/s . 5,45 s
xe = xOG – 2 m/s . ( 5,45 s – 4 s ) |
|
|
¡Listo! Encontramos un sistema de tantas ecuaciones como incógnitas (2x2); acá terminó la física. Lo que resta es álgebra. Y es una papa. Con la primera ecuación averiguamos la posición de encuentro: |
|
|
|
|
|
Con ese valor vamos a la segunda ecuación y hallamos la posición de la ventana opuesta.
8,175 m = xOG – 2 m/s . ( 5,45 s – 4 s )
8,175 m = xOG – 2 m/s . 1,45 s
8,175 m = xOG – 2,90 m
8,175 m + 2,90 m = xOG
|
|
|
|
|
|
Si te hubieses olvidado de poner el instante inicial de la garrafa... el ejercicio habría salido mal. ¿De qué estaríamos hablando en ese caso? De un error garrafal. |
|
|
DESAFIO: No te rías y hacé los gráficos. |
|
 |
| |
| Algunos derechos reservados.
Se permite su reproducción citando la fuente. Última actualización ago-13. Buenos Aires, Argentina. |
|
|
| |
|

