CINEMATICA, No me salen 46, practica online de fisica

más de cinemática

otros temas de Física

lecciones del maestro Ciruela

tonterías

NO ME SALEN
EJERCICIOS RESUELTOS DE FÍSICA
(Movimiento uniforme)

NMS c2.13 - ¿En qué se diferencias los gráficos de los movimientos uniformes que poseen diferentes t_o, x_o y v?

Este ejercicio es muy aleccionador. No dejes de aprovecharlo al detalle. Fijate que lo que el enunciado nos pide que variemos son las constantes de la ecuación horaria del MRU, que acá te resalto en rojo:

x = x_o + v ( t – t_o )

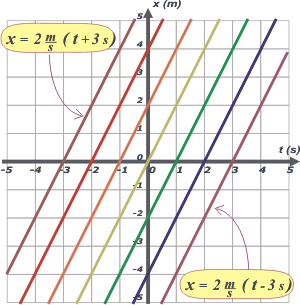
Efecto de t_o

Para investigar cuál es el efecto de t_o voy a dejar fijas las otras dos constantes en un valor cualquiera. En este caso voy a hacer x_o = 0 m y v = 2 m/s.

Todas estas gráficas representan movimientos cuyas ecuaciones horarias son de este tipo:

x = 2 m/s ( t – t_o )

En lo único que difieren entre ellos es t_o. De izquierda a derecha tienen estos valores:

-3 s, -2 s, -1 s, 0 s, 1 s, 2 s, 3 s.

Son todas paralelas, ya que la inclinación está dada por la velocidad que, en este caso, es la misma para todos.

No caigas en esta trampa: todas las rectas cortan al eje de las x justo en el valor de t_o; pero eso ocurre sólo porque en el ejemplo

que te propuse elegí el valor de x_o igual a cero. Si hubiese elegido un valor distinto de cer las rectas no cortarían al eje x en el valor t_o de cada una.

Efecto de x_o

Para investigar cuál es el efecto de x_o voy a dejar fijas las otras dos constantes en un valor cualquiera. En este caso voy a hacer t_o = 0 s y v = 2 m/s.

Todas estas gráficas representan movimientos cuyas ecuaciones horarias son de este tipo:

x = x_o + 2 m/s . t

En lo único que difieren entre ellos es x_o. De izquierda a derecha tienen estos valores:

6 m, 4 m, 2 m, 0 m, -2 m, -4 m y -6 m.

Son todas paralelas, ya que la inclinación está dada por la velocidad que, en este caso, es la misma para todos: 2 m/s.

Tal vez ya te hayas dado cuenta

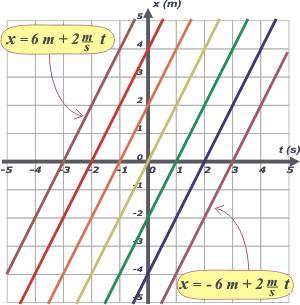
de que estas gráficas son idénticas que las anteriores. Eso nos dice que los mismos movimientos se pueden representar con diferentes ecuaciones horarias. Pero no es cierto: cada movimiento tiene una y solo una ecuación horaria que lo representa, pero esa ecuación horaria se puede escribir de infinitas maneras posibles. Mirá la recta violeta, la del extremo derecho. Arriba la representamos así: x = 2 m/s ( t – 3 s). Y acá así: x = -6 m + 2 m/s . t. No dudarás que:

2 m/s ( t – 3 s) = -6 m + 2 m/s . t

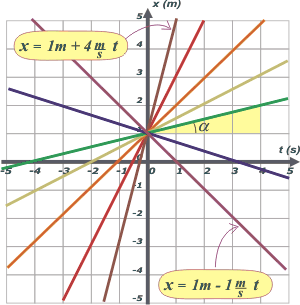
Y si dudás, podés operar algebraicamente y verificar que ambas expresiones son idénticas.

Efecto de v

Para investigar cuál es el efecto de v voy a dejar fijas las otras dos constantes en un valor cualquiera. En este caso voy a hacer x_o = 1 m y t_o = 0 s.

Todas estas gráficas representan movimientos cuyas ecuaciones horarias son de este tipo:

x = 1 m + v . t

En lo único que difieren entre ellos es v. De la marrón (cartel de arriba) hasta la violeta (cartel de abajo):

4 m/s, 2 m/s, 1 m/s, 0,5 m/s, 0,25 m/s, –0,33 m/s y –1 m/s.

Hemos roto el paralelismo. La velocidad va representada con la inclinación de la curva (en este caso rectas). Más paradita cuanto mayor es la velocidad, más acostada cuanto menor es la velocidad.

Hacia arriba (creciente) si la velocidad es positiva y hacia abajo (decreciente) si la velocidad es negativa. Es importante que aprendas a trazar gráficos a mano alzada, o sea, sin representar puntos.

Los matemáticos suelen llamar pendiente a la inclinación de la curva. Si llamamos α al ángulo que la recta forma con el eje x, entonces, por definición trigonométrica:

tg α = op / ady = Δx / Δt

(Mirá, por ejemplo, el triangulito amarillo que se corresponde con la recta verde).
¡Pero eso no es otra cosa que la velocidad!

tg α = v = Δx / Δt

Bueno, hasta acá llegamos.

DESAFIO: Graficá a mano alzada y en un mismo gráfico: x = 4 m + 0,5 m/s . t y
x = -2 m + 3 m/s . t.