 |
NO ME SALEN
EJERCICIOS RESUELTOS DE FÍSICA DEL CBC
(movimientos concatenados uniformes)
|
|

|
NMS c2.10*- Una persona dispara hacia una campana escuchando el impacto de la bala 1,89 segundos después de efectuar el disparo. Suponiendo que la velocidad de la bala es constante, de 200 m/s, y la velocidad del sonido también lo es y vale 340 m/s, calcular la distancia entre la persona y la campana.
|
Este problema me lo envió Anahí (que firma así: ø¤º°`°º¤øANAHIø¤º°`°º¤ø), una estudiante que se quejaba porque intentó resolverlo ochocientas mil veces (lo que se dice una mujer insistente). |
|
|
Acá tenés dos móviles: la bala (B) y el sonido (S). El movimiento del sonido comienza justo cuando termina el de la bala. Dibujé la trayectoria de la bala en rojo y el regreso del sonido en verde. Es cierto que el sonido viaja desde la campana en todas direcciones; pero a nosotros sólo debe interesarnos la dirección que regresa hasta donde está el observador tomando tiempos con un cronómetro: ¿lo ves?
Tomé un SR orientado hacia la derecha (ojo: hay que usar el mismo SR para todo el problema, si no... viene el cuco y te comerá). Llamé O al instante del disparo, C a la situación en la que la bala impacta en la campana, y F al instante en que se escucha el campanazo. |
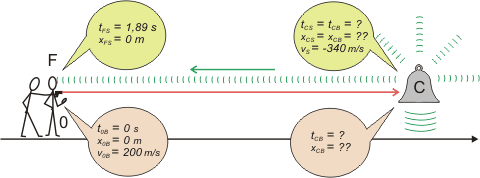 |
Lo más importante de los esquemas son los datos (o incógnitas) que consignás en los globitos. Es recontra importante que les pongas nombres claros y valores correctos. Un error acá... y fuiste, nada te salva. El globito rosa de abajo a la izquierda lo voy a usar para armar la ecuación horaria de la bala, y el globito verde de la derecha para la ecuación del sonido, cuyos modelos son
x = xo + v ( t – to )
ya que ambos se mueven con MRU. Es facilísimo hacerlo: reemplazo las constantes (lo que está en azul) haciendo CTRL+C y CTRL+V. Un juego de niños. Fijate cómo quedan |
|
|
| bala |
|
x = 200 m/s t |
|
| sonido |
|
x = xCB – 340 m/s ( t – tCB ) |
|
|
|
Ahora le pido a esas ecuaciones -que describen todo el movimiento de los dos móviles- que hablen exclusivamente de los sucesos que me interesan: la de la bala va a hablar del impacto en la campana y, la del sonido, de la llegada al oído del observador. Fijate que cuando se usa una ecuación horaria, cuando se especializa para un suceso en particular... sólo se reemplazan las variables |
|
| bala |
 |
xCB = 200 m/s tCB |
hablando de C |
| sonido |
0 m = xCB – 340 m/s ( 1,89 s – tCB ) |
hablando de F |
|
|
Lo sospeché desde un principio: irremediablemente desembocamos en un sistema de dos ecuaciones con dos incógnitas... se acabó la Física, se viene el álgebra...
En la ecuación del sonido reemplazo xBc por lo que indica la de la piedra:
0 m = 200 m/s tCB – 340 m/s ( 1,89 s – tCB )
0 m = 200 m/s tCB – 642,6 m + 340 m/s . tCB
642,6 m = 540 m/s tCB
tCB = 1,19s
con este valor vuelvo a la ecuación de la bala y obtengo |
|
|
|
| ¡Puntería el hombre! |
|
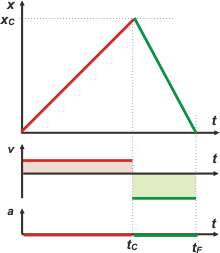 |
DESAFIO: (para hacer mentalmente) ¿Cuánto tarda el sonido en llegar desde la campana hasta el observador? ¿Cuál de las dos áreas sombreadas es mayor, la rosa o la verde? |
| |
| *Ejercicio tomado de Apuntes Teóricos de Biofísica, de Edu-Car. |
|
| |
Algunos derechos reservados.
Se permite su reproducción citando la fuente. Última actualización ago-07. Buenos Aires, Argentina. Vencimiento mayo de 3667. |
|
 |
|

