CINEMATICA, Ad 11, ejercicios resueltos

home

más de cinemática

otros temas de Física

lecciones del maestro Ciruela

tonterías

NO ME SALEN
PROBLEMAS RESUELTOS DE FÍSICA DEL CBC
(Movimiento uniforme)

NMS c2.01 - Un colectivo y un camión que pasan en el mismo momento por dos lugares separados 400 km marchan con velocidades constantes del mismo valor y de sentido contrario tardando tres horas en cruzarse. Si uno de ellos duplicara su velocidad tardarían en encontrarse:
a) 1 h b) 1,25 h c) 1,5 h
d) 2 h e) 2,5 h f) 4 h
SUGERENCIA: Intente resolver el problema desde un sistema fijo a Tierra y también desde un sistema fijo a uno de los móviles

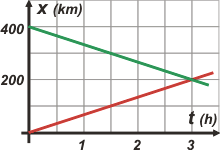
Voy a alterar el orden en el método No me salen. El motivo es que quiero mostrarte que a veces nos plantean ejercicios tan sencillos -física y numéricamente- que parece que lo que se pretende es que manejes las magnitudes en la mente y no en el papel. Eso tiene sus costado útil... hay cosas de las que se toma consciencia cuando se las baraja en el aire.

Vamos a empezar por lo último: lo gráficos... y vas a ver que la respuesta está tan al alcance que no vale la pena plantear ecuaciones.

Acá representamos las posiciones de los dos vehículos (no importa cuál es cuál) viajando a velocidades constantes de igual módulo y dirección, y de sentido contrario.

Se nota que ambos marchan con la misma rapidez porque realizan el mismo desplazamiento en el mismo tiempo. Por ejemplo: ambos recorren 100 km en el mismo intervalo: una hora y media.

Las inclinaciones de la grafícas son iguales (sólo que una es ascendente o positiva y la otra descendente o negativa).

Ahora cambia la situación, y a caballo de ese cambio viene una pregunta. Si la situación cambia debe cambiar el gráfico. Vamos a suponer que el móvil que duplica su velocidad es el representado en rojo.

Cómo hacer la nueva inclinación correctamente para poder leer el respuesta en el gráfico. Un modo sencillo es el siguiente: lo que antes recorría en un tiempo ahora lo recorre en la mitad de tiempo. Por ejemplo: el rojo recorría 200 km en 3 horas, ahora lo hará en una hora y media (mirá los dos circulitos).

El gráfico muestra claramente cuándo se produce el encuentro.

t_e = 2 h

opción d)

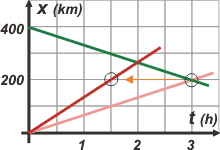
Se ve claramente porque el autor del ejercicio eligió números enteros y redondos como para que no haya dudas en la resolución gráfica, o para que sea sencillo en la resolución mental con operaciones de proporciones. Pero ya no es tan sencillo decir en qué posición se encontraron los vehículos. Vamos a la resolución tradicional.

La primera situación se representa con estas dos ecuaciones:

verde

rojo

x = 400 km – v t

x = v t

Y la segunda situación, por éstas:

verde

rojo

x = 400 km – v t

x = 2 v t

Si esas ecuaciones hablaran de las situaciones de los encuentros, dirían:

x_e = 400 km – v . 3 h

x_e = v . 3 h

x_e' = 400 km – v t_e'

x_e' = 2 v . t_e'

[1]

[2]

[3]

[4]

para el primer encuentro utilicé el subíndice e, y para el encuentro cuando el rojo tiene una velocidad doble e'

Ahí tenés cuatro ecuaciones con cuatro incógnitas. Una papa. Igualo las dos primeras y despejo v.

400 km – v . 3 h = v . 3 h

400 km = v . 6 h

v = 400 km / 6 h

Ahora igualo las dos últimas y reemplazo v por lo que acabo de obtener.

400 km – v t_e' = 2 v . t_e'

400 km = 3 v . t_e'

400 km = 3 (400 km / 6 h) . t_e'

De acá t_e'...

t_e' = 400 km /3 (400 km / 6 h)

t_e' = 2 h

(Ya lo sabíamos). Con ese valor volvemos a la ecuación [4] (también podríamos ir a la [3])...

x_e' = 2 (400 km / 6 h) . 2 h

x_e' = 2 (400 km / 6 h) . 2 h

x_e' = 267 km

Si quisieras resolver el ejercicio siguiendo la sugerencia del enunciado tendría que encontrar la ecuación del movimiento relativo. En el primer caso la velocidad de encuentro es 2v, y en el segundo caso, la velocidad de encuentro es 3v. El resto te lo dejo a vos. (Si todavía no viste movimiento relativo, no te preocupes, es sencillo; Cuando lo hayas hecho volvé para acá).

DESAFIO: ¿Cuánto vale la velocidad de cada vehículo en el primer caso?