NO ME SALEN
PROBLEMAS RESUELTOS DE FÍSICA DEL CBC
(Cinemática vectorial) |
|

|
 |
NMS 1.7 - Una hormiga se mueve por el borde superior
del pizarrón. A las 11:40 h se encuentra en el
punto A, 50 cm a la derecha del centro C del mismo.
A las 11:41 h está en B, 80 cm a la derecha de
C. A las 11:43 h es vista nuevamente en A, y a las
11:46 h se mete en una grieta que hay en D,
40 cm a la izquierda de C.
Elegir un sistema de referencia, origen y sentido
positivo, y:
a - Confeccionar una tabla de valores de posición
de la hormiga-tiempo, con la información
disponible.
b - Trazar un gráfico posición-tiempo. (¿Puede
completarlo?; ¿se puede saber dónde estaba la
hormiga a las 11:42 h?; ¿se puede saber a qué hora
u horas estaba en C ?).
c - Calcular la velocidad media de la hormiga
entre los siguientes instantes: 11:40 h y 11:41 h;
11:40 h y 11:43 h; 11:43 h y 11:46 h. Interpretar.
d - ¿Puede trazarse un gráfico que represente
velocidad media de la hormiga en función del
tiempo? ¿Por qué?. |
|
Hormiguita viajera... veamos qué podemos hacer con este ejercicio.
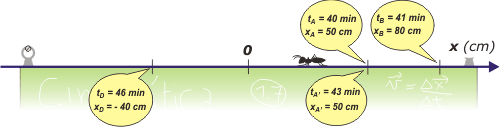
Lo primero que hay que hacer en éste o en cualquier otro ejercicio de cinemática es un esquema. Si no saabés lo que es un esquema, al menos, podés empezar por un dibujo que cuente lo mismo que el enunciado. Qué te parece éste: |
|
|
 |
|
|
No es exactamente un esquema... pero es un buen comienzo. Un esquema contiene el SR (sistema de referencia) elegido, nombres para las posiciones, instantes, etcétera. |
|
|
 |
|
Detalles y aclaraciones. Habrás visto que el enunciado no te indica qué SR elegir. Bueno yo elegí (vos podrías haber elegido otro) uno que tiene el cero de las posiciones en el punto C, horizontal con sentido positivo hacia la derecha medido en centímetros. Para la medición del tiempo elegí el cero a las 11 en punto del día de la hormiga.
Fijate que como la hormiga regresa sobre sus pasos (¿sabías que las hormigas tienen 6 patas?) los eventos de la ida no pueden tener el mismo nombre que los de vuelta, de modo que llamé A' al evento en que la hormiga vuelve a pasar por el punto A. |
|
| La tabla de valores es una pavada atómica. Consiste en volcar la información ordenada de esta manera. Ojo, debe ser la misma información que consta en el esquema. Nunca te olvides de consignar las unidades en una tabla de valores. Si quisieras agregar el nombre de cada evento podrías agregar una tercera columna primero. En nuestro caso, serían: A, B, A' y D. |
| x (cm) |
t (min) |
| 50 |
40 |
| 80 |
41 |
| 50 |
43 |
| -40 |
46 |
|
|
|
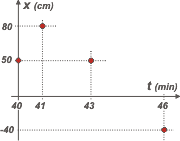
Este el gráfico que nos muestra la misma información que la tabla (y no más, porque estaríamos inventando). Cada punto rojo nos dice lo mismo que un renglón en la tabla de valores.
No se puede agregar más nada. No se pueden unir los puntos. No se puede saber a qué hora (en qué minuto) la hormiga pasó por C. odo lo que sabemos del movimiento es lo que aporta el enunciado. Además las hormigas son locas. |
 |
|
|
Las velocidades medias sí se pueden calcular. Nos piden varias.
Entre A y B. |
|
| vAB = |
|
ΔxAB |
= |
xB — xA |
= |
80 cm — 50 cm |
= |
30 cm |
= 30 cm/min |
|
|
|
|
| ΔtAB |
tB — tA |
41 min — 40 min |
1 min |
|
|
| Entre A y A'. |
|
|
|
|
|
|
|
| |
| vAA' = |
|
ΔxAA' |
= |
xA' — xA |
= |
50 cm — 50 cm |
= |
0 cm |
= 0 cm/min |
|
|
|
|
| ΔtAA' |
tA' — tA |
43 min — 40 min |
3 min |
|
|
|
| Entre A' y D. |
|
|
| vA'D = |
|
ΔxA'D |
= |
xD — xA' |
= |
- 40 cm — 50 cm |
= |
- 90 cm |
= - 30 cm/min |
|
|
|
|
| ΔtA'D |
tD — tA' |
46 min — 43 min |
3 min |
|
|
|
| Ese gráfico que te piden... es muy complicado y no aporta buena interpretación de la información. Hay otros más útiles. Ni te lo muestro. |
|
|
| DESAFIO: confeccionar un gráfico posición tiempo (de los infinitos posibles) que complete la información del movimiento de la hormiga . Si el que hacés no hace otra cosa que unir con rectas las cuatro informaciones de las que disponemos... dejás de tenerme como amigo... ¡Un poco más de creatividad, Ché! |
|
 |
| |
| Algunos derechos reservados.
Se permite su reproducción citando la fuente. Última actualización dic-13. Buenos Aires, Argentina. |
|
|
|

