 |
NO ME SALEN
PROBLEMAS RESUELTOS DE FÍSICA DEL CBC
(Cinemática vectorial)
|
|
 |
 |
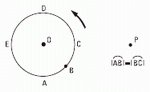
NMS 1.3- Un chico se encuentra en una calesita, de
modo que describe una circunferencia de 2 metros
de radio, dando 1 vuelta cada 8 segundos.
En la figura se esquematiza su trayectoria, vista
desde arriba. Considerando un único giro de la
calesita: |
 |
a - Adoptar un sistema de coordenadas centrado
en el punto O. Dibujar y determinar los vectores
posición del chico en los puntos A, B, C, D y E.
b - Determinar y representar los vectores desplazamiento
entre los puntos A y E; A y D; A y C;
A y B.
c - Determinar y representar en otro esquema
los vectores velocidad media entre los puntos A
y D, entre A y C y entre A y B.
d - Determinar y representar los vectores posición
de los puntos A, C y D, desde un sistema de
coordenadas en el mismo plano de la trayectoria,
centrado en el punto P, que está a 10 metros
de O. Comparar los resultados con los del inciso
a -.
e - Hallar los vectores desplazamiento y la velocidad
media entre los puntos A y D, y entre A y
C, en este nuevo sistema, y comparar con los resultados
hallados en b - y c -.
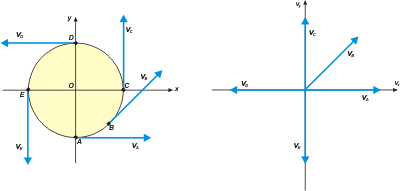
f - Representar los vectores velocidad instantánea
en los puntos A, B y C. ¿Dependen del sistema
de referencia elegido? ¿Cuál es su intensidad? |
Largo como esperanza de pobre... pero no tenemos más remedio. Empecemos. |
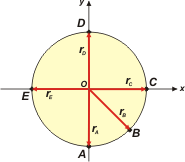 |
a -
rA = 0 m î — 2 m ĵ
rB = 1,41 m î — 1,41 m ĵ
rC = 2 m î + 0 m ĵ
rD = 0 m î + 2 m ĵ
rE = — 2 m î + 0 m ĵ
|
|
|
El valor 1,41 lo sacás haciendo pitágoras en el triangulito rectángulo que forma rB con los ejes. De ese trangulito sabés que la hipotenusa vale 2 y que los catetos son iguales. El arco AB es igual al arco BC (dato del enunciado dado en el esquemita). |
î y ĵ son vectores de módulo 1, se llaman versores y tienen por objeto contagiar el carácter vectorial a un valor y decir para dónde apunta. Suelen representarse con un sombrerito o una comita arriba (en lugar del punto típico de la i y la j). El versor î tiene la misma dirección y sentido que el eje x, y el versor ĵ que los del eje y.
b - El vector desplazamiento, ΔrAE, por ejemplo, es la resta vectorial entre los vectores posición posterior menos anterior (final menos inicial), rE — rA; para hallarlo hay que restar componente a componente. Fijate cómo salió, no necesito explicarte, es fácil.
ΔrAE = rE — rA
ΔrAE = (— 2 m î + 0 m ĵ ) — (0 m î — 2 m ĵ ) = — 2 m î + 2 m ĵ
Lo mismo hago con los otros.
ΔrAD = 0 m î + 4 m ĵ
ΔrAC = 2 m î + 2 m ĵ
ΔrAB = 1,41 m î + 0,59 m ĵ
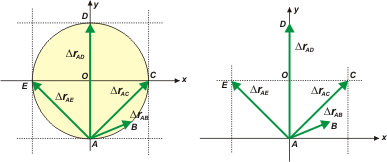
Lo representé en verde, igual que al resto. Los voy a representar dos veces. La de la izquierda es la operación geométrica: para restar dos vectores alcanza con unir ambos extremos. El vector resta siempre tiene origen en el primero y extremo en el segundo (origen en el sustraendo y extremo en el minuendo).
En el de la derecha los representé tal como resultaron analíticamente, entonces aparecen centrados en el origen del SR. Miralo bien, ahí los tenés. |
|
|
 |
|
|
c - La velocidad media es
vm = Δr / Δt
Para obtener al vector vm analíticamente se divide cada componente del vector Δr por el intervalo de tiempo, que para cada posición es diferente, pero es fácil de calcular, porque si tarda 8 s en dar una vuelta completa, tarda 4 en dar media, y así. |
|
|
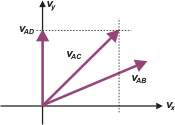 |
Represento a los tres en un gráfico de velocidades; fijate que la escala de este gráfico no tiene nada que ver con la de los anteriores.
vmAD = 0 m/s î + 1 m/s ĵ
vmAC = 1 m/s î + 1 m/s ĵ
vmAB = 1,41 m/s î + 0,59 m/s ĵ
|
|
|
|
| d - El gráfico está un poco fuera de escala, pero igual se entiende. Si no, no entraba. |
|
|
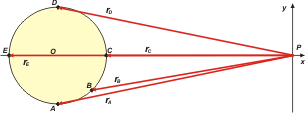 |
rA = —10 m î — 2 m ĵ
rB = —8,59 m î — 1,41 m ĵ
rC = —8 m î + 0 m ĵ
rD = —10 m î + 2 m ĵ
rE = — 12 m î + 0 m ĵ |
|
|
|
e - Si hacés las cuentas vas a ver que los resultados (y las representaciones) son las mismas que obtuvimos antes.
f - La velocidad instantánea la obtengo dividiendo el desplazamiento (medido sobre la trayectoria) con el intervalo de tiempo correspondiente. Por ejemplo para pegar una vuelta completa, o sea, recorrer 12,56 m (3,14 por diámetro) utiliza 8 s. Luego la velocidad instantánea vale v = 1,57 m/s. Te hice dos representaciones: una in situ, o sea, en la calesita; la otra, en un gráfico de velocidades. |
|
|
 |
|
|
Una vez más podrás notar que la escala que utilizo para las longitudes no tiene nada que ver con la escala que utilizo para las velocidades. Así debe ser.
DESAFIO: Obtené los módulos de todos los vectores que aparecen en este problema, comparalos entre sí, y hallá los ángulos que forman con el eje x. Y después, sí, andate de vacaciones a las islas Canarias. |
|
 |
| Algunos derechos reservados.
Se permite su reproducción citando la fuente. Última actualización ene-07. Buenos Aires, Argentina. |
|
|
|

