 |
NO ME SALEN
EJERCICIOS RESUELTOS DE FÍSICA
(Movimiento circular)
|
|

|
| |
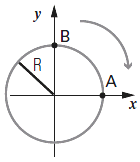
FIS c6.25 - En una autopista circular de 7,5 m de radio
dos competidores prueban sus motocicletas.
Ambos giran en sentido horario.
Uno de ellos, Gino, prueba su moto partiendo
de A realizando un movimiento
circular uniforme de
frecuencia igual a 30 r.p.m. El otro, Miguel, realiza un
movimiento uniformemente
acelerado, cuya aceleración
angular es de πrad/s².
Miguel pasa por B con una
velocidad angular de πrad/s en el mismo instante en el que Gino parte de A.
|
a) Escribir las ecuaciones horarias θ(t) para
cada una de las motos (especifique claramente
cómo mide el ángulo θ). Hallar el instante y la
posición en la cual ambos vehículos se encuentran
por primera vez .
b) Calcule los vectores velocidad y aceleración
de cada moto en el instante de encuentro.
Represéntelos en un esquema. ¿Cuál es la velocidad
relativa de Gino respecto de Miguel?
|
 |
|
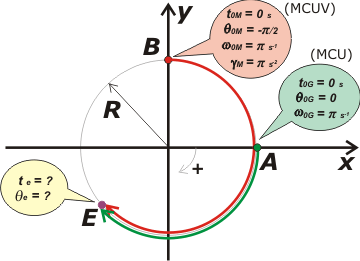 |
Si no hacemos un buen esquema este ejercicio se convierte en una pesadilla. Bueno, acá lo tenés Fijate que ya está elegido el sistema de referencia tanto de tiempos como de posiciones angulares (0 en A).
El encuentro no ocurre necesariamente en el lugar que lo consigné, pero bueno, todavía no podemos saberlo. |
Arranquemos junto con Gino que realiza un MCU. Sus ecuaciones son sencillas, nos dan la velocidad angular y la posición inicial. Entonces no tenemos que hacer ningún cálculo, excepto pasar su velocidad, 30 r.p.m., a radianes por segundo:
ωG = 30 . 2π / 60 s = π s-1
Ahora sí, escribamos sus ecuaciones horarias: |
|
|
| |
| |
θG(t) = π s-1 . t
ωG(t) = π s-1
γG = 0 |
|
a) |
|
|
|
Vamos con Miguel que realiza un MCUV y es más loquito. Tomamos el 0 de los tiempos cuando Miguel pasa por B. En ese instante Gino está en A y Miguel en B, tomamos el 0 de las posiciones en A. Y en ese instante la velocidad angular de Miguel es dato del ejercicio, πrad/s:
ωM = π s-1 + π s-2 t
γM = π s-2
Para encontrar la ecuación de posición angular tenemos que integrar la función velocidad angular de Miguel:
θM(t) =∫(π s-1 + π s-2 t) dt = π s-1 t + 0,5 π s-2 t2 + CθM
conociendo la posición inicial de Miguel en el instante 0 podemos hallar el valor de la constante de integración CθM.
θM(0s) = π s-1 . 0 s + 0,5 π s-2 (0 s)2 + CθM = − 0,5 π
CθM = − 0,5 π
Ahora ya tenemos las tres ecuaciones de Miguel: |
|
|
| |
| |
θM(t) = − 0,5 π + π s-1 t + 0,5 π s-2 t2
ωM(t) = π s-1 + π s-2 t
γM = π s-1 |
|
a) |
|
|
|
Para conocer el instante, te, en que los dos motociclistas se encuentran basta con pedirle a sus ecuaciones de posición angular que hablen de ese instante:
θG(te) = π s-1. te
θM(te) = − 0,5 π + π s-1 te + 0,5 π s-2 te2
Una papa algebraica. Igualemos las ecuaciones:
π s-1. te = − 0,5 π + π s-1 te + 0,5 π s-2 te2
0 = − 0,5 π + 0,5 π s-2 te2
te2 = 0,5 π / 0,5 π s-2
|
|
|
|
|
|
Si metemos ese valor en las ecuaciones de posición angular de cada motociclista deberíamos hallar el mismo resultado, ¿no?
θG(1s) = π s-1. 1 s
θM(1s) = − 0,5 π + π s-1 1 s + 0,5 π s-2 1 s2
|
|
|
|
|
|
O sea, se encuentran justo cortando al eje x en su rama negativa. Acordate de esto porque va a ser importante para establecer los vectores velocidad y aceleración.
b) Calcule los vectores velocidad y aceleración
de cada moto en el instante de encuentro.
Represéntelos en un esquema. ¿Cuál es la velocidad
relativa de Gino respecto de Miguel? Ahora le damos entrada a las otras ecuaciones (en cada una reemplazamos t por 1 s, o sea, el instante de encuentro, e). Empecemos con Gino: |
|
|
| |
| |
ωGe = π s-1
vGe = ωGe . R = π s-1. 7,5 m = 23,55 m/s ĵ
aGe = ωGe2 . R = π2 s-2. 7,5 m = 73,95 m/s2 î |
|
b) |
|
|
|
| Vamos ahora con Miguel (no te ovides que Miguel tiene aceleración tangencial debido a que aumenta su rapidez y centrípeta debido a que gira): |
|
|
| |
| |
ωMe = π s-1 + π s-2 1 s = 2 π s-1
vMe = ωMe . R = 2 π s-1. 7,5 m = 47,1 m/s ĵ
acMe = ωMe2 . R = 4 π2 s-2. 7,5 m = 295,79 m/s2 î
atMe = γM R = π s-2 . 7,5 m = 23,55 m/s2 ĵ
aMe = 295,79 m/s2 î + 23,55 m/s2 ĵ |
|
b) |
|
|
|
 |
|
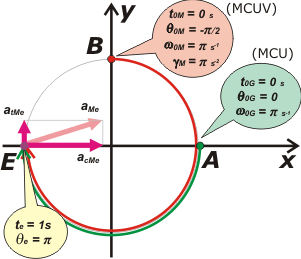
En este nuevo gráfico te representé la posición de encuentro correctamente ubicada y las componentes del vector aceleración de Miguel, y su vector aceleración (en una escala aproximada).
La aceleración de Gino es puramente centrípeta... la podés imaginar vos. |
|
|
| Finalmente nos piden la velocidad relativa entre ambos motociclistas: |
|
|
| |
| |
vGMe = (vMe − vGe ) = 23,55 m/s ĵ
|
|
b) |
|
|
|
|
|
|
DESAFIO: ¿Con qué diferencia de tiempo pasan por el punto B? |
|
 |
| Algunos derechos reservados (en criollo: no podés publicarlo a tu nombre, ¿entendiste? Mirá que tengo un boga repesado, ¿eh?).
Eso sí, se permite su reproducción citando la fuente, o sea, papá. Se agradece a Alejandro Ferreira por el envío de una errata. Última actualización mar-16. Buenos Aires, Argentina. |
|
|
| |
|

