NO ME SALEN
PROBLEMAS RESUELTOS DE FÍSICA DEL CBC
(Movimiento uniforme)
|
|

|
| |
FIS c5.08 - Las coordenadas de un ave que vuela en el
plano xy son:
x = 2,0 m – 3,6 m/s. t
y = 1,8 m/s². t²
a) Dibujar la trayectoria del ave.
b) Calcular los vectores velocidad y aceleración
en función del tiempo.
c) Dibujar los vectores velocidad y aceleración
para t = 3 s.
En ese instante, el ave ¿está acelerando, frenando
o su rapidez no está cambiando?
d) Calcule los vectores desplazamiento, velocidad
media y aceleración media en el intervalo
comprendido entre los instantes t = 0 s y t = 3 s. |
|
¿Pero qué hace este ejercicio mezclado con los de tiro oblicuo? El ave no realiza un movimiento libre... pero fijate, no sólo se trata de un movimiento bidimensional sino que en una dimensión se comporta como uniforme y en la otra como variado... exactamente como los tiros oblicuos. y como siempre, empezaremos con un esquema. |
|
|
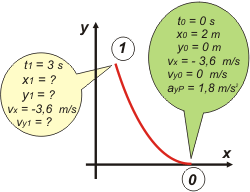 |
Sé que la trayectoria es una parábola porque es eso lo que le ocurre a los tiros oblicuos y a cualquier otro movimiento que en una dimensión es uniforme y en la otra variado. Sé que arranca hacia la izquierda porque en x tiene una velocidad hacia la izquierda y en y parte del reposo.
No sé cuánto recorrió en 3 segundos, pero a los fines del esquema no importa.
Toda esa información la saqué de las ecuaciones horarias que nos da el enunciado: |
|
|
|
x = 2,0 m – 3,6 m/s . t
y = 1,8 m/s² . t²
A esas ecuaciones les pedimos que no hablen del instante 1, 3 segundos.
x1 = 2,0 m – 3,6 m/s . 3 s
y1 = 1,8 m/s² . 9 s²
Y obtenemos:
x1 = – 8,8 m
y1 = 16,2 m
En cuanto a las velocidades, en la dirección x sabemos que es constante. pero en la dirección y va aumentando y el enunciado no nos lo cuenta, pero recordamos que si tenemos la función que describe posición, podemos obtener la de velocidad derivando:
y' = vy = 3,6 m/s². t
vx = – 3,6 m/s
Si lo querés en forma vectorial acá lo tenés:
|
|
|
| |
v(t) = – 3,6 m/s î + 3,6 m/s². t ĵ |
|
|
|
|
| Y la aceleración: |
|
|
|
|
|
También podemos calcular las componentes de la velocidad en 1.
vx = – 3,6 m/s
vy = 3,6 m/s². 3 s = 10,8 m/s
Y para calcular los vectores medios hay que hacer restas:
Δr01 = r1 – r0 = – 8,8 m î + 16,2 m ĵ – (2 m î + 0 m ĵ )
|
|
|
| |
Δr01 = – 10,8 m î + 16,2 m ĵ |
|
|
|
|
| La velocidad media la obtenemos dividiendo el desplazamiento por e intervalo de tiempo: |
|
|
| |
vm01 = – 3,6 m/s î + 5,4 m/s ĵ |
|
|
|
|
La variación de velocidad otra simple resta:
Δv01 = v1 – v0 = – 3,6 m/s î + 10,8 m/s ĵ – (– 3,6 m/s î + 0 m/s ĵ )
Δv01 = 0 m/s î + 10,8 m/s ĵ
Y la aceleración media la obtenemos dividiendo la variación de velocidad por el intervalo correspondiente: |
|
|
|
|
|
| Ave que comió, voló. |
|
|
Desafío: La ecuación de la trayectoria. |
|
 |
| |
|
| Algunos derechos reservados.
Se prohibe estrictamente leer este ejercicio resuelto por encima: hay que leerlo despacio y con atención. Las penalizaciones a esta infracción son severísimas. Se permite su reproducción citando la fuente. Última actualización mar-16. Buenos Aires, Argentina. |
|
|
| |
|

