home  | más de cinemática | otros temas de Física | lecciones del maestro Ciruela | tonterías |  @ 

  NO ME SALEN
  PROBLEMAS RESUELTOS DE FÍSICA
   (Tiro oblicuo)

  

manolito
 

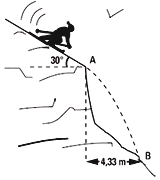
FIS c5.04 - Un esquiador que se desliza por una rampa, inclinada 30º, llega al borde A con cierta velocidad. Luego de 1 segundo de vuelo libre, retoma la pista en B, 4,33 m más adelante del punto A.
Hallar la velocidad que tiene en el punto A, y el desnivel entre A y B. ¿Qué velocidad tendrá en B?
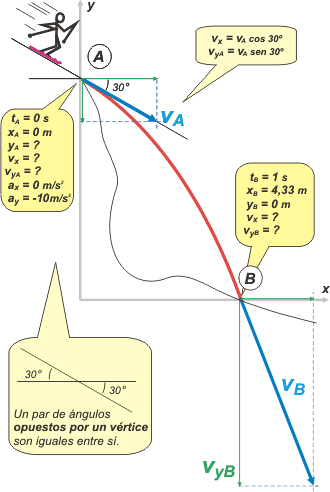
He aquí un típico ejemplo de ese fenómeno que los físicos llaman "el problema del esquiador que se está por hacer pelota". Un típico físico haría un típico esquema.

Cinemática - No me salen - Ricardo Cabrera

Elegí el origen del SR en ese punto porque fue el primero que se me ocurrió; no creo que sea más conveniente que otro. Aquí, nuevamente, la redacción del problema induce a pensar que lo que ocurre antes del punto A es fundamental para resolverlo, y por ello son varios los que pisan el palito y plantean cuestiones que tienen que ver con el movimiento sobre la rampa. Lo cierto es que el problema se resuelve perfectamente tomando como que empieza en A, con ciertas características iniciales, como ser el ángulo inicial (30º, ¿viste?), velocidad inicial (vA) distinta de cero, etc. Ya todo figura en el esquema, para eso está.

¿Cuántas ecuaciones describen el problema? Tres, muy bien, como en todo TO hay que reemplazar las constantes (to , xo , yo , vx , voy , y g) en las ecuaciones generales de los movimientos correspondientes.
cuando armás un esquema al mismo tiempo estás eligiendo un Sistema de Referencia

x = xo + vx ( t – to )

y = yo + voy ( t – to ) + ½ g ( t – to )²

vy = voy+ g ( t – to )

  
Las constantes iniciales en este caso pueden ser las del punto A. Nuestras ecuaciones, entonces, son:  

x = vA cos 30º . t

y = yA – vA sen 30º . t – 5 m/s² . t²

vy = – vA sen 30º – 10 m/s² . t
Estas son las ecuaciones que describen TODO el fenómeno del movimiento contado en el enunciado
Y ahora las usamos, es decir, les pedimos que "hablen" del punto B y, si todo anduvo bien, debería estar resuelto el problema.  
  4,33 m = vA . 0,866 . 1 s   [1]
  0 m = yA – vA . 0,5 . 1 s – 5 m/s² . 1 s²   [2]
  vyB = – vA . 0,5 – 10 m/s² . 1 s   [3]
Estas solo hablan de los instantes que nos interesan

Efectivamente, quedó un sistema de tantas ecuaciones como incógnitas donde las incógnitas, si sabemos interpretarlas, son las que pide el enunciado del problema.

Aquí va una resolución de las 279 posibles. De la ecuación [1] despejamos vA y calculamos:

    
  vA = 5 m/s  
   
reemplazo este valor en [2] y en [3]    
  yA = 7,5 m  
 

Siendo yA = 0 m, 7,5 m es el desnivel que nos están pidiendo en el enunciado, y por eso lo recuadré. Te diste cuenta ya, que siempre recuadro aquellos resultados que pide el enunciado... y sólo esos, ¿no?

   
  vyB = – 12,5 m/s  
   

Recordando que vx = vA cos 30º

    
  vx = 4,33 m/s  
   
Ya tenemos dos de las respuestas: la velocidad en A y el desnivel, que es yA. La velocidad en B todavía no la tenemos, pero sí sus componentes... luego, aplicando el teorema de Pitágoras...    
   
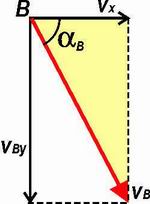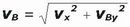vB = – 13,23 m/s    
De yapa (¿sabés lo que es la yapa?):
αB = arc tg ( vyB / vx )    
αB = 71º    
     
 

no te pierdas mi novela
DESAFIO: Rehacer con un SR cuyo origen esté en A y apunte (sentido positivo) hacia abajo. Ah, y falta hacer los gráficos, tanto para el planteo resuelto como para el desafío. ¡Mirá que son distintos!   Ricardo Cabrera
Prohibida la comercialización de este material didáctico. No apto para machete. Las transgresiones a esta disposición serán penalizadas con la misma condena que le impusieron a Galileo Galilei: leer la Biblia. Sólo se permite su reproducción citando la fuente. Todos los derechos reservados. Última actualización ago-06. Buenos Aires, Argentina.