NO ME SALEN
PROBLEMAS RESUELTOS DE FÍSICA DEL CBC
(Movimiento de tiro oblicuo)
|
|

|
| |
FIS c5.01- Un arquero dispara desde el piso una flecha
cuya velocidad de salida es de 50 m/s y forma un
ángulo de 37º con la horizontal.
Considerando despreciable el rozamiento con
el aire, y utilizando un sistema de coordenadas
con el î hacia el lado del lanzamiento y el ĵ hacia
arriba, calcular:
a) El tiempo que la flecha está en el aire.
b) La altura máxima.
c) El alcance.
d) El vector velocidad a los 5 segundos.
e) El vector velocidad final.
f) Los vectores desplazamiento, velocidad
media y aceleración media en los intervalos
comprendidos entre los instantes 0 s y thmáx ;
y entre 0 s y talcance.
|
|
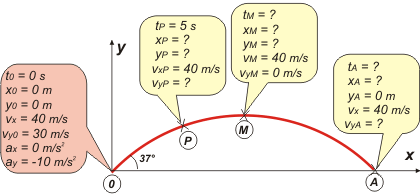
Uh, qué despelote. Pongamos las cosas claras con un esquema: |
|
|
 |
|
|
Fijate si toda la información del enunciado está bien volcada. (El esquema también sirve para eso, para contrastar la información del enunciado con tu propia interpretación). Bueno, creo que está todo bie. No se puede saber a priori dónde está la flecha a los 5 segundo, la puse por ahí nomás, a ese evento lo llamé P, y los resultados dirán si estaba ahí o no, pero no importa. La velocidad inicial la consigné con sus componentes:
v0x = v0 cos 37º = 40 m/s
v0y = v0 sen 37º = 30 m/s
Durante todo el vuelo la única aceleración en la de la gravedad y con este sistema de referencia es negativa. Bueno. Sigamos; Hay que escribir las ecuaciones horarias y para eso hay que tener los modelos a la vista:
x = xo + vx ( t – to )
y = yo + voy ( t – to ) + ½ g ( t – to )²
vy = voy+ g ( t – to )
Si reemplazamos las constantes con cuidado de no equivocarnos, sacándolas del globito rosa, es imposible equivocarse:
x = 40 m/s t
y = 30 m/s t – 5 m/s² t²
vy = 30 m/s – 10 m/s² t
Y ahora le pedimos a esas ecuaciones que hablen de los puntos en los que tenemos algún interés: P, M y A. (A lo tonto, sin pensarlo, copiando de los globitos amarllos). |
|
|
| P |
xP = 40 m/s 5 s |
[1] |
| P |
yP = 30 m/s 5 s – 5 m/s² 25 s² |
[2] |
| P |
vyP = 30 m/s – 10 m/s² 5 s |
[3] |
| M |
xM = 40 m/s tM |
[4] |
| M |
yM = 30 m/s tM – 5 m/s² tM² |
[5] |
| M |
0 m/s = 30 m/s – 10 m/s² tM |
[6] |
| A |
xA = 40 m/s tA |
[7] |
| A |
0 m = 30 m/s tA– 5 m/s² tA² |
[8] |
| A |
vyA = 30 m/s – 10 m/s² tA |
[9] |
|
|
|
Bueno, ya está, fue todo muy mecánico. El único lugar donde tuve que exprimir un poco el cerebro fue en el esquema, el resto una papa.
Ah... querés que te resuelva el sistema... bueno, ahí va: de la [8] calculás tA: |
|
|
|
|
|
Para calcular la altura máxima calcuamos tM con la [6] y lo que nos da lo metemos en la [5]:
tM = 3 s
|
|
|
|
|
|
yM = 15 m
Para calcular el alcance, xA , ponemos tA en la [7] y calculamos:
|
|
|
|
|
|
Para calcular la velocidad a los 5 segundos vamos a la [5]...
vyP = – 20 m/s
Y recordando que la velocidad de traslación horizontal es constante, ya puedo responder cuán es el vector velocidad en ese instante:
vP = 40 m/s î – 20 m/s ĵ
|
|
|
| |
vP = 40 m/s î – 20 m/s ĵ |
d) |
|
|
|
| Si lo querés responder en componentes polares sacás el módulo con Pitágoras y el ángulo con el arcotangente. |
|
|
| |
|vP| = 44, 7 m/s ; αP = –26,6º |
d) |
|
|
|
Y el vector velocidad final , A, de la misma manera. Primero vas a la [9]:
vyA = – 30 m/s
|
|
|
| |
vA = 40 m/s î – 30 m/s ĵ |
e) |
|
|
|
| |
|vP| = 50 m/s ; αA = –37º |
e) |
|
|
|
El último ítem nos pide desplazamientos, velocidades medias y aceleraciones medias. Empecemos por los desplazamientos:. Tenemos las posiciones: 0: (0 ; 0), M: (120 ; 45) y P: (240 ; 0). Entonces los desplazamientos serán (lo obtenemos restando miembro a miembro):Δ |
|
|
| |
Δr0M: (120 ; 45) m ; Δr0A: (240 ; 0) m |
e) |
|
|
|
| Vamos con las velocidades medias en esos dos mismos intervalos, basta con dividir los desplazamientos por los intervalos de tiempo de cada uno (3 segundos para el primero, 6 segundo para el otro). |
|
|
| |
vm0M: (40 ; 15) m/s ; vm0A: (40 ; 0) m/s |
e) |
|
|
|
Y las aceleraciones medias requieren que previamente conozcamos las velocidades.
v0: (40 ; 30) m/s, vM: (40 ; 0) m/s y vA: (40 ; –30) m/s. Ahora sí, las restas:
Δv0M: (0 ; –30) m/s; Δv0A: (0 ; –60) m/s
Y la aceleración media la obtenemos dividiendo esas variaciones de velocidad por el intervalo de tiempo considerado. |
|
|
| |
am0M: (0 ; –10) m/s² ; am0A: (0 ; –10) m/s² |
e) |
|
|
|
| Hay mucho para discutir. Para empezar viste que el punto P no estaba donde lo pusimos sin ya casi volviendo al piso. No importó para nada, el esquema nos sirvió como organizador del trabajo. Habrás visto que los tiempos y las posiciones horizontales y los módulos de las velocidades verticales presentan una estricta simetría en torno al eje de la parábola de la trayectoria, ¿no?. En general trato de no utilizar esa propiedad y resuelvo los ejercicios sólo con las propiedades cinemáticas, dejando las geométricas para casos de emergencia. Bueno, seguí disfrutándolo. |
|
|
Desafío: Mentalmente: la velocidad media de todo el movimiento. |
|
 |
| |
|
| Algunos derechos reservados.
Se prohibe estrictamente leer este ejercicio resuelto por encima: hay que leerlo despacio y con atención. Las penalizaciones a esta infracción son severísimas. Se permite su reproducción citando la fuente. Última actualización mar-16. Buenos Aires, Argentina. |
|
|
| |
|

