home  | más de cinemática | otros temas de Física | lecciones del maestro Ciruela | tonterías |  @ 

   NO ME SALEN
  PROBLEMAS RESUELTOS DE FÍSICA DEL CBC
   Movimiento variado (con análisis matemático)

  

manolito

 

FIS c4.27 - Una partícula se desplaza siguiendo una trayectoria rectilínea. Para cada una de las siguientes expresiones de la aceleración a(t) de la partícula, encontrar la expresión más general para la velocidad v(t) y la posición x(t).
    a) a(t) = ao , donde ao es una constante.
    b) a(t) = ao cos ω t, donde ao y ω son constantes.
    c) a(t) = A t², donde A es una constante.

Ah, bueno... esto es nuevo. Pero se trata del camino inverso que recorrimos en los ejercicios anteriores. En ellos partíamos de la función posición y arribábamos a la función aceleración, y lo lográbamos derivando. Acá debemos partir de la aceleración (nos dan tres casos) y debemos llegar a la velocidad y posición. Lo lograremos integrando.

    
Arranquemos: a(t) = ao

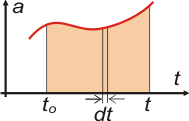
Recordemos que un cambio de velocidad, (v – vo ), lo podemos calcular integrando el área bajo la curva de aceleración (o sea sumando los infinitos rectángulos de base dt y altura a) entre dos valores de tiempo: uno de referencia to y otro cualquiera t. Analíticamente, la integral definida entre esos dos valores:
   
    v – vo = ∫ t ao dt   =   ao t + C

t  =   ao (t – to)
   
to to
   

Si queremos la función de v para cualquier instante, basta con pasar vo sumando al primer miembro.

    
  v(t) = vo + ao (t – to) a)
   

Que es la recontra archi conocida (por vos) segunda ecuación horaria (v) de los movimientos uniformemente variados, o sea, con aceleración constante (que es una condición expresamente indicada en el enunciado).

Hacemos lo mismo para obtener la función de posición:

    
    x – xo = ∫ t (vo + ao (t – to)) dt   =   vo t + ½ ao t² – ao to t + C

t   
   
to to
   

x – xo = vo t + ½ ao t² – ao to t + C – vo to – ½ ao to² + ao to²– C

x – xo = vo t + ½ ao t² – ao to t– vo to – ½ ao to² + ao to²

x – xo = vo ( t – to ) + ao ( ½ t² –  to t  + ½ to² )

x – xo = vo ( t – to ) + ½ ao ( t² – 2 to t  + to² )

x – xo = vo ( t – to ) + ½ ao ( t – to )²

Despejamos x y ya:

    
  x(t) = xo + vo (t – to) + ½ ao (t – to)² a)
   

Que es la archi-híper conocida que ya utilizaste 200.000 veces.

    
   
Vamos a la segunda: a(t) = ao cos ω t    
    v – vo = ∫ t ao cos ω t dt   =   (ao/ω) sen ω t + C

t  
   
to to
   

v – vo = (ao /ω) [sen (ω t) – sen (ω to)]

Y como antes:

    
  v(t) = vo + (ao /ω) [sen (ω t) – sen (ω to)] b)
   
Ahora la ecuación de posición:    
    x – xo = ∫ t (vo + (ao /ω) [sen (ω t) – sen (ω to)]) dt   =    
 
to
   
    x – xo = vo t – (ao /ω²) [cos (ω t)] – [(ao /ω) [sen (ω to) t ] + C

t  
 
to
   

De donde:

    
 

x(t) = xo + vo (t – to) – ( ao /ω²) [cos (ω t) – cos(ω to)] –

– (ao /ω) sen (ω to) (t – to)

 b)
   
   
Vamos al último: a(t) = A t²    
    v – vo = ∫ t A t² dt   =    (A/3) t³ + C

t  =   (A/3) (t³ – to³)
   
to to
   
Y despejando v:    
  v(t) = vo + (A/3) (t³ – to³) c)
   
Finalmente la ecuación de posición:    
    x – xo = ∫ t   [ vo + (A/3) (t³ – to³)] dt
 
to
   
    x – xo =  vo t – (A to³/3) t + (A/12) t4 + C

t  
 
to
   
Y despejando x:    
  x(t) = xo + (vo – A to³/3) (t – to) + (A/12) (t4– to4) c)
   
Mortal.    

Desafío: No... si llegaste hasta acá estás eximido de todo desafío.

  Ricardo Cabrera
   
Algunos derechos reservados. Se prohibe estrictamente leer este ejercicio resuelto por encima: hay que leerlo despacio y con atención. Las penalizaciones a esta infracción son severísimas. Se permite su reproducción citando la fuente. Se agradece a la ingeniera Cintia Perrone por el envío de una errata. Última actualización mar-16. Buenos Aires, Argentina.