NO ME SALEN
PROBLEMAS RESUELTOS DE FÍSICA DEL CBC
(Movimiento variado)
|
|

|
| |
Fc3.23 - Las ecuaciones de movimiento para dos
partículas A y B que se mueven en la misma
dirección son las siguientes:
xA(t) = 3,2 t² – 6 t − 20
xB(t) = 29 + 8,5 t − 4,1 t²,
donde x se mide en metros y t en segundos.
a) Calcular el instante y la posición en el cual
las partículas se encuentran.
b) Calcular las velocidades de A y B en el instante
de encuentro.
c) Graficar aceleración, velocidad y posición
en función del tiempo. |
|
Ah, bueno... nos sorprendió. Veamos qué es esto. Nos dan las ecuaciones horarias de dos móviles y lo primero que nos preguntan es dónde se encuentran Eso ya lo hicimos 59 veces, simplemente le pedimos a esas ecuaciones que hablen del encuentro, xE y tE , y nos fijamos si se pueden encontrar esos valores (seguro que sí). ¿Probamos?
xE = − 20 – 6 tE + 3,2 tE²
xE = 29 + 8,5 tE − 4,1 tE²
Parece que sí, porque son dos ecuaciones con dos incógnitas. Pura álgebra. Usemos el método de igualación.
3,2 tE² – 6 tE − 20 = 29 + 8,5 tE − 4,1 tE²
7,3 tE² – 14,5 tE − 49 = 0
Usando la ecuación de los griegos de resolución de cuadráticas, resulta:
tE1 = – 1,78 y tE2 = 3,77
Con esos valores volvemos a las ecuaciones para conocer las posiciones: |
|
|
| |
tE1 = – 1,78 s ; xE1= 0,85 m |
aproximadamente |
|
|
|
| |
tE2 = 3,77 s ; xE2= 2,8 m |
aproximadamente |
|
|
|
O sea, se pueden encontrar en dos oportunidades.
Para calcular las velocidades con las que se encuentran necesitamos las segundas ecuaciones horarias, las de velocidad, pero no las tenemos. No hay problema, justo acá nos acordamos que la función derivada de la posición es la función velocidad.
xA(t) = 3,2 t² – 6 t − 20
x'A(t) = vA(t) = 6,4 t – 6
Ahora las del móvil B.
xB(t) = 29 + 8,5 t − 4,1 t²
x'B(t) = vB(t) = 8,5 − 8,2 t
A esas dos ecuaciones les preguntamos cuánto vale la velocidad en el instante de encuentro (voy a hacerlo sólo para tE2.
vAE2 = 6,4 . tE2 – 6
vBE2 = 8,5 − 8,2 tE2
|
|
|
| |
vAE2 = 18,13 m/s ; vBE2 = – 22,41 m/s |
aproximadamente |
|
|
|
| Y grafiquemos: |
|
|
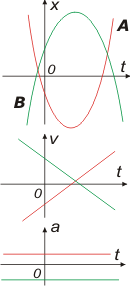 |
Bueno, ahí los tenés, bastante aproximados y en tándem.
Aprovechá para mirar los detalles, las posiciones e instantes de los encuentros, los ceros de la velocidad, las pendientes y concavidades, las velocidades en los encuentros... en fin, todo lo que aprendiste de funciones y de cinemática hasta ahora.
Que te aproveche.
|
|
|
|
| |
|
|
| |
Desafío: Las aceleraciones de ambos. |
|
 |
| |
|
| Algunos derechos reservados.
Se prohibe estrictamente leer este ejercicio resuelto por encima: hay que leerlo despacio y con atención. Las penalizaciones a esta infracción son severísimas. Se permite su reproducción citando la fuente. Última actualización mar-16. Buenos Aires, Argentina. |
|
|
| |
|

