| home | | | más de cinemática | | | otros temas de Física | | | lecciones del maestro Ciruela | | | tonterías | | | @ |
|
||||||||||||||
|
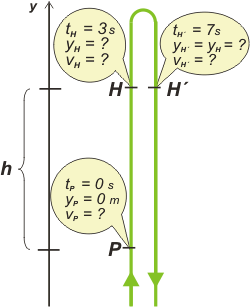
En realidad el cuerpo sube y baja por la misma recta. Lo dibujé así porque esto es un esquema (je, je), para que no se me encimen los puntos de los que quiero hablar. Fijate que pasa por la altura H en dos instantes, uno al subir, otro al bajar. Es necesario, entonces, ponerles distinto nombre. Los llamé tH y tH'. La elección del SR es arbitraria. Elegí ése porque supuse que vos elegirías el mismo. A partir de esa elección sabemos que la aceleración del móvil será, para todo el movimiento, g = -10 m/s2 , tanto a la subida como a la bajada. |
|
Las ecuaciones horarias las hallamos, como siempre, reemplazando en los modelos del M.R.U.V. (¿los tenés a mano?) las constantes "iniciales" (como ves, no necesariamente son verdaderamente iniciales), en este caso las del punto p. |
||
|
||
Y ahora... ¡las usamos! (¡Qué aburrido, todos los problemas se hacen igual!. ¡Al final en el parcial no me van a poder sorprender con nada!) Le pedimos a la ecuación de posición que hable de los puntos H y H'. A la de velocidad le damos descanso. |
||
| yH = vP . 3 s – 5 m/s² . (3 s)² | ||||
| yH = vP . 7 s – 5 m/s² . (7 s)² | ||||
¡No me digas, ya sé: dos ecuaciones con dos incógnitas! Y además bastante sencillo. |
||||
| vP . 3 s – 5 m/s² . (3 s)² = vP . 7 s – 5 m/s² . (7 s)² | ||||
| vP . (3 s – 7 s) = 5 m/s² . (9 s2 – 49 s²) | ||||
| vP = 200 m / 4 s | ||||
| vP = 50 m/s | (Qué notable) | |||
|
|
DESAFIO: A ojo y sin hacer ninguna cuenta, decir en qué instante pasa por la altura máxima; después sí, calcularla. Decir a ojo, y sin hacer ninguna cuenta, cuánto vale la velocidad al regresar a P. Calcular las velocidades vH y vH'. |
 |
|
|