NO ME SALEN
PROBLEMAS RESUELTOS DE FÍSICA DEL CBC
(Movimiento variado)
|
|

|
| |
c3.16. Desde una terraza a 40 m del suelo se lanza
una piedra verticalmente hacia arriba con velocidad
de 15 m/s.
Despreciando el rozamiento con el aire:
a) Calcular el módulo, dirección y sentido de la
posición, de la velocidad y de la aceleración en el
instante t = 3 s.
b) ¿Cuándo llega al suelo?
c) ¿Cuándo y dónde se encuentra con una piedra
arrojada desde el suelo verticalmente hacia arriba
con una velocidad de 55 m/s y que parte desde el
suelo en el mismo instante que la anterior?
d) Representar gráficamente la posición, la
velocidad y la aceleración en función del tiempo. |
|
| Como siempre (bueno... casi siempre) vamos a arrancar con un buen esquema... no un dibujito cualunque: un esquema completo, un verdadera herramienta cinemática. |
|
|
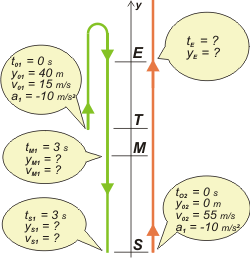 |
A ver si te cierra. Elegí uns SR positivo hacia arriba con el cero en el suelo, S, y 40 metros en la terraza, T.
Hay una piedra que se lanza hacia arriba desde la terraza, su trayectoria en verde. Entre otras cosas se pregunta dónde está a los 3 segundos de ser arrojada. Bien, no lo sé, voy a tratar de averiguarlo, pero a ese evento lo llamé M y ya sabremos es es más arriba o más abajo de donde lo representé.
En rosa la otra piedra que sale desde abajo con mayor velocidad. En algún momento se cruzan. A ese evento lo llamé E. No sé si es antes o después de que la primera piedra pegue la vuelta hacia abajo, pero tampoco importa, no es asunto del esquema, que está para otra cosa. |
|
|
|
Fijate que a ambas piedras les asigné una aceleración de -10 m/s², ya que no depende de qué haga cada piedra, sino del sistema de referencia elegido. Si el sistema apunta hacia arriba, g es negativo.
Bueno, tengamos los modelos de ecuaciones a mano:
y = yo + vo ( t – to ) + ½ g ( t – to )²
v = vo + a ( t – to )
Te escribí las variables en azul y las constantes en negro. Reemplazamos las constantes (es facilícimo si hiciste un esquema. Las constantes están en el globito inicial de cada móvil. Fijate:
y = 40 m + 15 m/s t – 5 m/s² t²
v = 15 m/s – 10 m/s² t
y = 55 m/s t – 5 m/s² t²
v = 55 m/s – 10 m/s² t
Mirá qué chuchi: te escribí nuevamente las variables en color, pero las de cada móvil con el propio. Bueno, ahora le pedimos a esas ecuaciones que hablen de los puntos que nos interesan, o sea, M, E y S.
Piedra 1 hablando de M: |
|
|
| |
y1M = 40 m + 15 m/s . 3 s – 5 m/s² 9 s²
v1M = 15 m/s – 10 m/s² . 3 s |
[1]
[2] |
|
|
|
|
| Piedra 1 hablando de S: |
|
|
| |
0 m = 40 m + 15 m/s . t1s – 5 m/s² t1s²
v1S = 15 m/s – 10 m/s² . t1s |
[3]
[4] |
|
|
|
|
| Piedra 1 hablando de E: |
|
|
| |
yE = 40 m + 15 m/s . tE – 5 m/s² tE²
v1E = 15 m/s – 10 m/s² . tE |
[5]
[6] |
|
|
|
|
| Piedra 2 hablando de E: |
|
|
| |
yE = 55 m/s . tE – 5 m/s² tE²
v2E = 55 m/s – 10 m/s² . tE |
[7]
[8] |
|
|
|
|
Bueno... el resto es álgebra (súper fácil), ya muy poco le queda de física. De la [1] y [2] calculamos las posición y velocidad de la piedra 1 en M. |
|
|
| |
y1M = 40 m , v1M = – 15 m/s |
|
|
|
|
| De la [3] calculamos t1s |
|
|
|
|
|
Con la [5] y la [7] juntas, calculamos yE y tE. Mirá, podemos igualarlas:
40 m + 15 m/s . tE – 5 m/s² tE² = 55 m/s . tE – 5 m/s² tE²
40 m + 15 m/s . tE = 55 m/s . tE
40 m = 40 m/s . tE
|
|
|
|
|
|
| Hacemos los gráficos: |
|
|
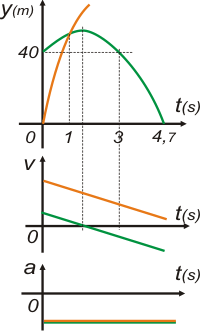 |
Bueno, ahí los tenés, bastante aproximados y en tándem.
Aprovechá para mirar los detalles, el paralelismo entre las gráficas de velocidad, la coincidencia en las gráficas de aceleración, la forma de las parábolas, la posición del punto más alto de la piedra 1, la simetría del moviemiento en torno al instante 1,5 s, en fin, tenés mucho para meditar.
Que te aproveche.
|
|
|
|
Desafío: ¿Es posible que haya un segundo encuentro suponiendo que vienen viajando desde tiempo inmemorial y que seguirán viajando por toda la eternidad? |
|
 |
| |
|
| Algunos derechos reservados.
Se prohibe estrictamente leer este ejercicio resuelto por encima: hay que leerlo despacio y con atención. Las penalizaciones a esta infracción son severísimas. Se permite su reproducción citando la fuente. Última actualización mar-16. Buenos Aires, Argentina. |
|
|
| |
|

