 |
NO ME SALEN
PROBLEMAS RESUELTOS DE FÍSICA
(Movimiento uniformemente variado)
|
|

|
| |
 |
F c3.12 - El conductor de un tren subterráneo de 40 m de longitud, y que marcha a 15 m/s, debe aplicar los frenos 50 m antes de entrar en una estación cuyo andén mide 100 m de longitud.
Calcular entre qué valores debe hallarse el de la aceleración de frenado, para que el tren se detenga dentro de los límites del andén. |
|
| Miremos un poquito los esquemas. Te hice un tren de tres vagones, como de domingo, quedó bonito, ¿no? |
|
|
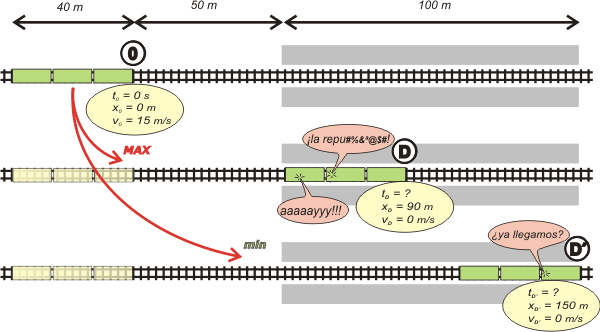 |
Entre la situación de frenado MAX y frenado min, hay muchas intermedias. En cualquiera de esas, el tren quedaría detenido en zonas intermedias del andén. MAX y min representan los modos extremos de frenado. Aquí, entonces, se nos presentan dos problemas independientes y hay que encararlos por separado. Son éstos:
1) hallar la máxima aceleración de frenado (aquella con la que el tren se detiene totalmente dentro del andén pero lo más "antes" posible, con una frenada brusca).
2) hallar la mínima aceleración de frenado (aquella con la que el tren se detiene totalmente dentro del andén, frenando suavemente, pero casi pasándose).
Los vamos a resolver al mismo tiempo, en dos columnas. Tomemos un punto cualquiera del tren (no se olviden que nuestra cinemática es "puntual"); por ejemplo el frente.
|
|
|
MAX
Como siempre, hay que tener a mano las ecuaciones generales del movimiento que nos ocupa, en este caso el MRUV.
Son dos:
x = xo + vo ( t – to ) + ½ a ( t – to )²
v = vo + a ( t – to )
En ellas reemplazamos las constantes
(to, xo, vo y a) por las constantes iniciales de nuestro tren. (Son las mismas para los dos casos)
x = 15 m/s . t + ½ aMAX t²
v = 15 m/s + aMAX t
Ahora le pedimos a cada ecuación que hable del único punto de interés que nos queda: el punto en que se detiene, D.
Ellas dicen: |
|
min
Como siempre, hay que tener a mano las ecuaciones generales del movimiento que nos ocupa, en este caso el MRUV.
Son dos:
x = xo + vo ( t – to ) + ½ a ( t – to )²
v = vo + a ( t – to )
En ellas reemplazamos las constantes
(to, xo, vo y a) por las constantes iniciales de nuestro tren. (Son las mismas para los dos casos)
x = 15 m/s . t + ½ amin t²
v = 15 m/s + amin t
Ahora le pedimos a cada ecuación que hable del único punto de interés que nos queda: el punto en que se detiene, D'. Ellas dicen: |
|
|
 |
90 m = 15 m/s . tD + ½ aMAX tD² |
| 0 m/s = 15 m/s + aMAX tD |
|
|
 |
150 m = 15 m/s . tD' + ½ amin tD'² |
| 0 m/s = 15 m/s + amin tD'· |
|
|
|
Y qué nos quedó: un sistema de dos ecuaciones con dos incógnitas entre las que se encuentra aMAX, y puede
obtenerse operando algebraicamente. Aquí entonces se terminó la física del problema, lo que queda no es tan dramático. Vamos a resolverlo.
De la segunda: tD = (-15 m/s) / aMAX
reemplazo esto en la primera y simplifico |
|
Y qué nos quedó: un sistema de dos ecuaciones con dos incógnitas entre las que se encuentra amin, y puede obtenerse operando algebraicamente. Aquí entonces se terminó la física del problema, lo que queda no es tan dramático. Vamos a resolverlo.
De la segunda: tD' = (-15 m/s) / amin
reemplazo esto en la primera y simplifico |
|
|
| |
|
|
|
|
| aMAX = – 1,25 m/s² |
|
amin = – 0,75 m/s² |
|
|
| |
|
|
|
|
| Me embola escribir m/s (metro sobre segundo) de esa forma, con la raya oblicua. Lo correcto es escribir la m justo arriba de la s y la raya horizontal. Lo mismo con 1/2 y para todas las expresiones fraccionarias. |
|
|
| Los gráficos los voy a hacer superpuestos, aunque sabemos que corresponden a movimientos diferentes y no simultáneos. |
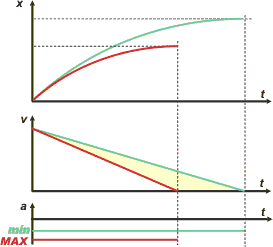 |
Esta disposición permite comparar más fácilmente los dos movimientos. Los colores verde y rojo repiten el código de todo el ejercicio.
El orden de los gráfico es siempre el mismo... vos ya sabés.
Sin hacer cuentas...
¿cuánto vale el área
del triangulito amarillo? |
|
|
|
DESAFIO: Averiguar con qué aceleración debe frenar el motorman (¿sabés quién es el motorman?) para que el subterráneo se frene justo en la mitad del andén, y resolverlo tomando to = 10 s y xo = 200 m. |
|
 |
| Algunos derechos reservados (para mí, lógico).
Se permite su reproducción clonal citando la fuente. Última actualización abr-07. Buenos Aires, Argentina. |
|
|
| |
|

