NO ME SALEN
PROBLEMAS RESUELTOS DE FÍSICA DEL CBC
(Movimiento variado)
|
|

|
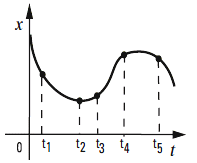
FIS c3.10 - La figura muestra un gráfico de posición, x,
en función del tiempo, t, para un móvil con movimiento
rectilíneo.
¿Cuáles son los signos de v y a en los instantes:
a) t1; b) t2 ;c) t3; d) t4 ; e) t5?
Indique si el móvil está disminuyendo o
aumentando el módulo de su velocidad en cada
uno de esos instantes. |
 |
|
| Vamos a hacer lo siguiente: una ampliación de cada instante con los tres gráficos (en tándem y un profundo análisis. Empecemos con el punto 1. Acompañame. |
|
|
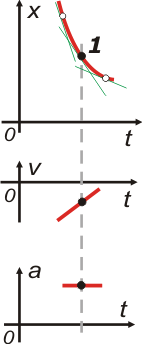 |
Si mirás a gráfica de posición es indudable que el móvil está retrocediendo (mientras avanza el tiempo las psiciones que son positivas dismunuyen acercándose al cero). Eso indica que la velocidad debe ser negativa y eso es lo que representé en el gráfico de velocidad.
¿Pero cómo varía la velocidad? Si volvemos a observar la gráfica de posición, fijate, tracé las tangentes a la gráfica en dos puntos de la vecindad de 1. A la izquierda (en un instante anterior a 1) la tangente está muy inclinada. A la derecha (en un instante posterior a 1) la tangente está bastante menos inclinada que en 1. Es obvio que la pendiente va disminuyendo a medida que avanza el tiempo (en un entorno de 1). Eso nos indica que la rapidez va disminuyendo, pero ojo, que la velocidad está aumentando, porque no te olvides que son velocidades negativas.
Por último, si la velocidad está aumentando la aceleración debe ser positiva. (lo que por otro lado nos recuerda eso de parábola sonriente, aceleración positiva).
Te aclaro que no sabemos si ese arco de curva que estamos analizando es o no es una parábola (la verdad es que no lo parece). De modo que no podemos asegurar que la curva de velocidad ni la de aceleración sean rectas. |
|
|
|
| Como mucho podemos afirmar que la función de la velocidad es uniformemente creciente, y nada más. pero en una primera aproximación al problema el análisis que hicimos es bastante aceptable. Vamos al punto 2. |
|
|
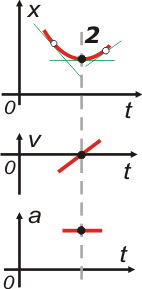 |
Bueno, vamos más rápido. En el instante 2 tenemos un mínimo (más propiamente un mínimo relativo o un mínimo local). En ese instante podemos observar que la inclinación de la tangente es nula (la tangente es horizontal). Eso nos indica que la velocidad vale 0. Y es justamente lo que muestra el gráfico de velocidad.
Si mirá un entorno cercano a 2, ves que en un instante anterior la posición decrece y en uno posterio aumenta. Lo cual se condice con el gráfico de velocidad: antes negativa y después positiva. Conclusión: la velocidad aumenta.
Finalmente, eso nos indica que la aceleración sigue siendo positiva, y es justamente lo representado en el gráfico de aceleración.
Nuevamente te advierto que no hay indicios de que v y a sean lineales, es sólo una aproximación para en pequeño entorno del punto en cuestión. |
|
|
|
| Vamos a punto 3. |
|
|
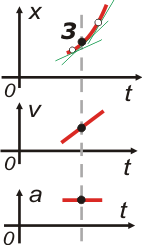 |
Esto ya se torna muy fácil: tangentes que se van poniendo cada vez más inclinadas, velocidad positiva y en aumento, aceleración positiva... etcétera.
Recordá las savedades que hicimos antes, también valen para éste.
Lamentablemente el ejercicio no te pregunta por el instante más interesante de todo el movimiento representado en la curva de posición. Se trata del punto en el que cambia la curvatura (para decirlo de un modo que te ayude a aproximarte: en el que pasamos de una parábola sonriente a una parábola triste). Está entre el 3 y el 4. Sean o no parábolas eso se llama punto de inflexión y requiere un análisis importante. Te la dejo picando para que no puedas dormir a la noche. |
|
|
|
| Vamos al 4 y al 5 juntos. |
|
|
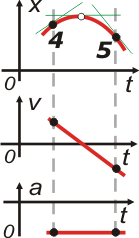 |
Acá tenés todo de vuelta para analiar en profundidad. Se incorporó un máximo relativo (si se tratase de una parábola lo llamaríamos vértice), en el que la velocidad vale cero.
Si mostrás ese ejercicio por ahí no te olvides de mencionar las salvedades que ya te repetí 37 veces: nada indica que las curvas sean arcos de parábolas, ni las de velocidad y aceleración sean rectas, o sea, son análisis aproximados (pero útiles).
Te deseo suerte con el asunto del punto de inflexión. Y que te garúe finito. |
|
|
|
| |
|
|
Desafío: Indicar si la velocidad media entre t1 y t5 es mayor, menor o igual a cero. |
|
 |
| |
|
| Algunos derechos reservados.
Se prohibe estrictamente leer este ejercicio resuelto por encima: hay que leerlo despacio y con atención. Las penalizaciones a esta infracción son severísimas. Se permite su reproducción citando la fuente. Última actualización mar-16. Buenos Aires, Argentina. |
|
|
| |
|

