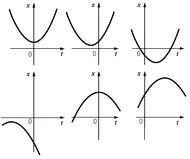
FIS c3.08 - Sin usar valores numéricos, en los siguientes gráficos de posición (x) en función del tiempo (t), determinar los signos de la posición, la aceleración (a) y la velocidad (v) en t = 0 s. Para cada caso graficar la velocidad y la aceleración en función del tiempo.

    No te preocupes, abajo están más grandes.

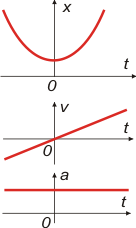Empecemos con este. Para empezar fijate que el enunciado no dice que las curvas sean parábolas. De modo que no sabemos exactamente qué tipo de movimiento representan, pero sea el que sea se parece mucho a un movimiento variado de aceleración constante.

En este ejercicio voy a hacer de cuenta de que lo son, efectivamente MRUV.

Eso me permite agregar un tercer gráfico para cada ítem, el de aceleración, que pongo siempre abajo.

Los detalles a los que tenés que prestar atención son: cuando la curva de posición alcanz el vértice justo está en el instante cero, y justo en ese instante la recta de velocidad también vale cero (la pendiente es horizontal, matemáticamente nula). En cambio la pendiente de la velocidad no es nula, por eso el gráfico de aceleración en ese instante es distinta de cero.

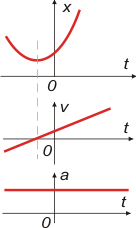Este es muy parecido al anterior... la supuesta parábola parece estar desplazada un poco hacia la derecha. En el instante cero corta al eje y en un valor positivo. Si miramos el gráfico de velocidad en ese instante vemos que indica un valor positivo.

Era lógico, ya que estamos en la rama ascendente de las posiciones.

Fijate la línea punteada, nuevamente, cuando la velocidad vale cero la la inclinación de la parábola es nula, estamos en su vértice. El móvil deja de retroceder y comienza a avanzar.

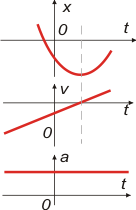Tampoco hay muchas diferencias con los anteriores. En t_o la pendiente en negativa, el móvil retrocede, luego la velocidad acusa valores negativos.

Fijate (en este y en los anteriores también) si la rapidez del movimiento va en aumento o en descenso... y corroborá que el módulo de la velocidad también va en aumento o en descenso.

Para los 3 que ya vimos, fijate que la velocidad (no la rapidez, que es el módulo de la veocidad) siempre aumenta, luego, en los tres la aceleración (supuestamente constante) siempre es positiva. (parábola sonriente, aceleración positiva).

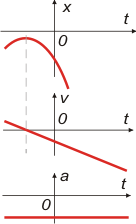Arrancamos con las que suponemos parábolas tristes. Ya mismo mirá la gráfica de aceleración... constante y negativa.

Nuevamente mirá el vértice de la parábola... no importa si indica una posición positiva o negativa, lo que importa es que ahí su velocidad vale cero y eso es lo que indica el gráfico de velocidad.

Podés mirá la correspondencia entre las tres magnitudes en el instante t_o.

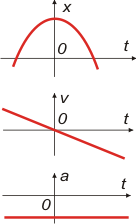Si analizaste a fondo el anterior, este es una pavada. Reforzá la siguiente idea: en el gráfico anterior cuando la velocidad del movil se anula la posición era negativa, y en este positiva. Sin embargo en ambos la gráfica de velocidad indica cero... ¡y claro!, si te está hablando de velocidad, no de rabanitos...

Volvé a observar cómo varía la velocidad en el de velocidad y cómo, en tiempos iguales, varía la pendiente de la gráfica de posición.

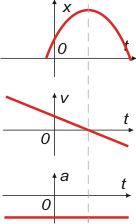De estos gráficos no te voy a decir nada... si hiciste bien la tarea con los anteriores, estos últimos te tienen que resultar una papa.

Lo que sí voy a hacer es reforzar la idea de gráficos en tandem. Cuando los gráficos se construyen en tandem en un sólo golpe de vista obtenés la información de las tres magnitudes importantes en la cinemática: posición, velocidad y aceleración.

El golpe de vista se realiza de esta manera: con una recta imaginaria vertical que atraviesa los tres gráficos (como te indiqué con la punteada). Por eso es importante que los 3 gráficos tengan la misma escala de tiempo.