NO ME SALEN
PROBLEMAS RESUELTOS DE FÍSICA DEL CBC
(Movimiento uniforme)
|
|

|
FIS c2.02- Un cuerpo que en el instante t = 0 se encuentra
en un punto A, viaja en línea recta con velocidad
constante de módulo desconocido v.
Cuando transcurre un tiempo T el móvil pasa
por un punto B que está a una distancia d de A.
a) Hallar v = f (d, T)
b) Dar dos expresiones para la posición del
cuerpo en función del tiempo, una considerando
un sistema de coordenadas con origen en A y
otra considerando un sistema de coordenadas
con origen en B, y graficarlas. |
|
| Si el móvil viaja a velocidad constante, esa velocidad podemos expresarla de esta manera, que ya queda en función de d: |
|
|
| |
|
|
Teniendo a mano el modelo de ecuación horario:
x = xo + v ( t – to )
Y considerando que to = 0 s, xo = A = 0 y v = d/T, nuestra ecuación quedará así: |
|
|
| |
|
|
Si cambiamos el sistema de referencia por uno que tenga la misma referencia de tiempos pero el cero de las posiciones en B, entonces: to = 0 s, xo = – d y v = d/T. |
|
|
| |
|
|
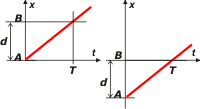 |
Acá está los gráficos, ambos describen el mismo movimiento, ambos utilizan la misma escala de tiempos y difieren, solamente, el la escala de posiciones, que sólo tiene corrido el 0 y utiizan la misma escala de longitud.
Ciertamente cada uno debería indicar dónde está el cero, pero nos permitimos la convención de que si no lo indicamos éste se halla en la intesección de los ejes.
|
|
|
|
| |
|
|
| |
|
|
Desafío: ¿Cómo quedarían las ecuaciones si d = 10 m y T = 1 s? |
|
 |
| |
|
| Algunos derechos reservados.
Se prohibe estrictamente leer este ejercicio resuelto por encima: hay que leerlo despacio y con atención. Las penalizaciones a esta infracción son severísimas. Se permite su reproducción citando la fuente. Última actualización mar-16. Buenos Aires, Argentina. |
|
|
| |
|

