 |
NO ME SALEN
PROBLEMAS RESUELTOS DE BIOFÍSICA DEL CBC
(Movimiento uniformemente variado)
|
|

|
| |
 |
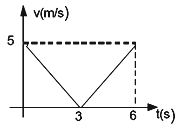
3) El gráfico representa la velocidad en función
del tiempo de un móvil que:
a) recorre 15 m en los primeros 3 s y en los
siguientes 3 s vuelve donde estaba.
b) recorre 7,5 m en los primeros 3 s y en los
siguientes 3 s vuelve donde estaba.
|
 |
c) recorre 15 m en los primeros 3 segundos y luego
otros 15 m en el mismo sentido, en los siguientes
3 segundos.
d) recorre 7,5 m en los primeros 3 segundos y luego
otros 7,5 m en el mismo sentido, en los siguientes
3 segundos.
e) retrocede 5m durante los primeros 3 segundos y avanza 5 m
durante los 3 segundos siguientes.
f) se mueve con aceleración constante durante los 6 segundos. |
|
Mirá... te propongo algo diferente: rehago el gráfico, y lo coloco en su tándem correspondiente posición-velocidad-aceleración... Eso me va a dar oportunidad de describir todas las connotaciones cinemáticas que -de última- nos va a llevar a la respuesta correcta.
| | |
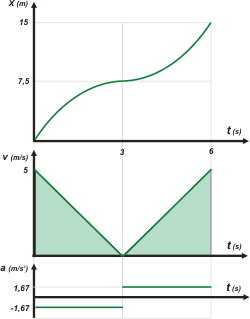 |
Al gráfico de velocidad le agregué color en las áreas encerradas bajo la curva. Esas áreas representan el desplazamiento correspondiente a cada intervalo. Además, vemos que representan desplazamientos positivos (avances) porque las áreas están colocadas sobre el eje de los tiempos. Esto se condice perfectamente con la observación de que las velocidades del gráfico son siempre positivas.
Las áreas -ambas- valen 7,5 metros. Se trata de dos triángulos de base 3 segundos, y 5 metros sobre segundo de altura. (Acordate que el área de un triángulo es igual al producto de base por la altura sobre dos).
Vamos a los gráficos de posición. El tramo que va de 0 a 3 s consiste en un avance desde la posición 0 hasta los 7,5 m. |
|
|
|
Se trata de un avance a velocidad menguante (decreciente), de modo que la inclinación debe ir "aplanándose" progresivamente.... y debe terminar a los 3 s, sin inclinación, horizontal... porque se corresponde con la velocidad cero. Supongo que ya te diste cuenta de que lo que estoy haciendo es describir un arco de parábola ascendente de concavidad negativa (triste).
El segundo tramo debe arrancar a los 7,5 m y terminar 7,5 metros más adelante, o sea, en 15 m. Como el anterior, también es de avance, pero con inclinación creciente. Arranca desde la horizontalidad y aumenta hasta estar tan inclinada como lo estuvo el tramo anterior en el instante inicial. Estamos frente a un arco de parábola ascendente de concavidad positiva (alegre).
Las aceleraciones son constantes, tanto la del primer tramo como la del segundo. Los valores los podemos calcular fácilmente haciendo:
|
|
|
| a2 = |
|
Δv |
= |
– 5 m/s |
= – 1,67 m/s2 |
|
|
| Δt |
3 s |
|
|
|
| a2 = |
|
Δv |
= |
5 m/s |
= 1,67 m/s2 |
|
|
| Δt |
3 s |
|
|
|
| Bueno... por todo lo discutido... deberás aceptar que la única proposición que se corresponde con la descripción del gráfico es la d). |
|
|
| Desafío: Hacer un gráfico velocidad-tiempo que coincida con cada una de las proposiciones distintas de la d). |
|
 |
|
|
|
| Algunos derechos reservados.
Se prohibe estrictamente leer este ejercicio resuelto por encima, hay que leerlo despacio y con atención. Las penalizaciones a esta infracción son severas. Se permite su reproducción citando la fuente. Última actualización jul-07. Buenos Aires, Argentina. |
|
|

