 |
NO ME SALEN
PROBLEMAS RESUELTOS DE BIOFÍSICA DEL CBC
(Movimiento uniformemente variado)
|
|

|
| |

|
16) Considerando un sistema de coordenadas positivo hacia arriba:
a) Representar velocidad en función del tiempo para un objeto que es arrojado hacia arriba, queda pegado en el techo durante unos instantes y luego cae.
b) Representar posición en función del tiempo para el mismo movimiento. |
No vas a creer todas las cosas que podemos discutir en los gráficos que describen la historia sencilla de este enunciado. Acá abajo te los hice; eso sí, no en el orden que nos lo piden sino en el orden lógico y correcto:
| | |
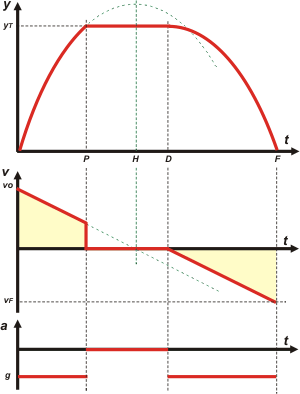 |
Empecemos analizando el gráfico de posición (en este caso: de alturas). Como ves, el objeto sale despedido desde el piso (desde el cero) y a medida que corre el tiempo va ascendiendo cada vez más lento, hasta que llega al techo (yT) y en ese instante, (P), choca y se queda pegado.
Fijate que para quedarse pegado al techo tiene que llegar ahí con cierta velocidad distinta de cero, si no... sería muy difícil pegarse.
Se queda ahí quietito y pegado, sin moverse, hasta que se despega (en el instante D) y se precipita nuevamente al suelo, descendiendo cada vez más rápido. ¿Lo ves?
Tanto el movimiento de ascenso como el de descenso son variados y con la misma aceleración (negativa); por lo tanto, se trata de dos arcos de la misma parábola de concavidad negativa (triste), aunque estos arcos se hallan desplazados. |
|
|
|
El primer arco -el que representa la subida- lo prolongué un poquito en punteada verde para que veas cómo hubiese seguido el vuelo del objeto si no hubiese estado el techo. Habría alcanzado una altura máxima en un instante hipotético (H), y en ese momento -recién ahí- su velocidad se habría anulado. A patir de ahí iniciaría el regreso como cualquier cuerpo que sube y baja.
Mirá bien la diferencia entre los puntos de la gráfica que se corresponden con el pegado y el despegado del techo. En el pegado hay un punto anguloso (así se llaman) ya que ese choque implica un cambio abrupto (pero no instantáneo) de velocidad. En cambio el punto de despegue se corresponde con una curvatura suave, ya que el techo no dispara el objeto hacia abajo, sino que lo suelta.
Ahora vamos al gráfico de velocidad. Parte de una velocidad positiva (vo) que desciende uniformemente (MRUV). En el instante en que el objeto toca el techo, cae abruptamente a cero. Así se mantiene mientras el cuerpo sigue pegado; y cuando se despega inicia el retorno partiendo desde el reposo y con velocidades crecientes... pero crecientes en módulo, ya que en el sistema de referencia que apunta hacia arriba todo movimiento hacia abajo se corresponde con velocidades negativas.
Te vuelvo a pegar los gráficos nuevamente así podemos proseguir la discusión sin que tengas que moverte hacia arriba a cada rato. Son los mismos. |
|
|
 |
Mirá un poco la recta oblicua que representa las velocidades de subida. Te la prolongué en punteadas verdes para que puedas apreciar dos cosas: lo primero es que intersecta al eje de los tiempos (o sea: se hubiese hecho cero) en el instante en que el objeto hubiese alcanzado su altura máxima si no había techo.
Lo segundo es que la gráfica de la subida es paralela a la gráfica de la bajada, lo cual es necesario, ya que la aceleración es la misma en ambos intervalos; por lo tanto, deben tener la misma pendiente.
(Tal vez recuerdes que siendo la aceleración la derivada de la velocidad, se debe corresponder -gráficamente- con la inclinación, o sea, la pendiente). |
|
|
|
Ahora mirá las áreas que te sombreé en amarillo. Deben ser iguales, ya que representan el mismo desplazamiento (uno de ida, y el mismo de vuelta; del piso al techo, y del techo al piso). Como no tenemos valores no podés hacer una comprobación numérica pero, si te animás, sí podés hallar una comprobación geométrica.
Fijate que el intervalo de bajada es mayor que el intervalo de subida. Eso es lógico ya que, habiendo partido del reposo, el descenso se realizó con menos rapidez. El asunto de los intervalos se nota -sobre todo- en el gráfico de aceleración-tiempo. El intervalo en el que el objeto está pegado al techo (P-D) es arbitrario y lo decidí yo a ojímetro.
Todavía podría agregar más comentarios sobre estos gráficos... por ejemplo por qué el salto de la velocidad está marcado, y los saltos de la aceleración no. Podríamos seguir cortando tela de este rollo infinito carillas y carillas, pero van a decir que soy un obsesivo. It's too much.
Eso sí: dejame aprovechar la volteada y plantear las ecuaciones, ¿dale? |
|
|
| |
| |
y = vo t – 5 m/s² t ² |
|
para 0 < t < P |
| |
v = vo – 10 m/s² t |
|
| |
y = yT |
|
para P < t < D |
| |
y = yT – 5 m/s² ( t – D)² |
|
para D < t < F |
| |
v = – 10 m/s² ( t – D) |
|
|
|
 |
Desafíos (tengo varios): El primero es que rehagas los gráficos, pero para un sistema de referencia que apunte hacia abajo y tenga el cero a la altura de la mesa, más o menos. El segundo es que escribas las ecuaciones de todo el movimiento pero descriptas bajo ese nuevo SR. El tercero es que demuestres gráficamente que las dos áreas sombreadas son iguales. El cuarto es que demuestres analíticamente que las dos áreas son iguales. Ninguno es imposible, creeme. |
|
|
|
| Algunos derechos reservados.
Se permite su reproducción citando la fuente. Aradezco el envío de una errata a la ingeniera Cintia Perrone. Última actualización sep-07. Buenos Aires, Argentina. |
|
|

