NO ME SALEN
PROBLEMAS RESUELTOS DE BIOFÍSICA DEL CBC
(Movimiento uniforme)
|
|

|
| |

|
7) Un objeto recorre 240 km en dos horas y luego 240 km más en tres horas.
a) Calcule el valor de la velocidad media en las dos primeras horas, en las tres últimas
y en el recorrido total.
b) Grafique la posición en función del tiempo. |
Mirá... vamos a hacer al revés, primero hacemos el gráfico y después vemos qué otra cosa. Vas a encontrar que las herramientas gráficas (ya sean los gráficos como los esquemas) nos permiten pensar, aclarar, discutir un montón de asuntos que si permaneciesen confusos o mal entendidos los ejercicios no salen por más fórmulas que tengas copiadas en tu machete.
| |
|
 |
|
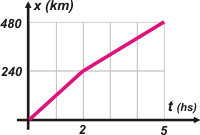
Mirá atentamente cada detalle y fijate si este gráfico dice exactamente lo mismo que el enunciado. (La respuesta es no, pero, por ahora, supongamos que sí).
Fijate que tomé arbitrariamente el cero de las posiciones y los tiempos en el inicio del primer movimiento que relata el enunciado. |
|
|
|
Es un detalle... pero igual te lo marco: fijate la primera recta, está más inclinada (tiene mayor pendiente) que la segunda... tiene su lógica, ¿no?
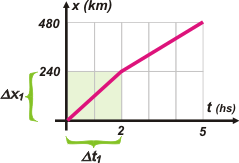
Bueno, vayamos a las preguntas. Nos piden la velocidad media del primer tramo, que llamaremos vm1. |
|
|
 |
|
Eso significa que debemos considerar solo el primer desplazamiento, que llamaré Δx1, y el intervalo de tiempo correspondiente, Δt1.
vm1 = Δx1 / Δt1
Reemplazando por los valores del ejercicio, tenemos: |
|
|
|
vm1 = (240 km – 0 km) /( 2 h – 0 h )
vm1 = 240 km /2 h
|
|
|
|
|
|
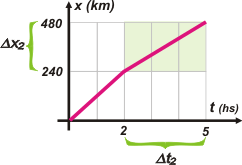
De la misma manera calculamos la velocidad media del segundo tramo, que llamaremos vm2. Prestá atención. |
|
|
 |
|
Eso significa que debemos considerar solo el segundo desplazamiento, que llamaré Δx2, y el intervalo de tiempo correspondiente, Δt2.
vm2 = Δx2 / Δt2
Reemplazando por los valores del ejercicio, tenemos: |
|
|
|
vm2 = (480 km – 240 km) /( 5 h – 2 h )
vm2 = 240 km /3 h
|
|
|
|
|
|
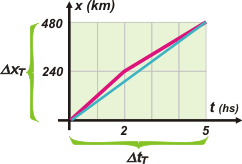
Y para calcular la velocidad media total, que llamaremos vmT, hay que proceder exactamente de la misma forma que antes, o sea... |
|
|
 |
|
Eso significa que debemos considerar todo el desplazamiento, que llamaré ΔxT, y el intervalo de tiempo correspondiente, ΔtT.
vmT = ΔxT / ΔtT
Reemplazando por los valores del ejercicio, tenemos: |
|
|
|
vmT = (480 km – 0 km) /( 5 h – 0 h )
vmT = 480 km /5 h
|
|
|
|
|
|
Fijate que la velocidad media total es un valor intermedio entre las otras velocidades... ¡pero no el promedio!
¿Y qué significado tiene esa velocidad media? No mucho, nos da una idea de "rapidez general, al bulto"... si querés (algunos lo dicen así, pero a mí mucho no me gusta) es la velocidad que tendría un móvil que viaja a velocidad constante con una velocidad igual a tu velocidad media y llega al mismo tiempo. Cuya representación gráfica sería la que hice en celeste.
Por último vamos a criticar el primer gráfico. Te acordás que te había anticipado que el gráfico (que ya sé, lo hice yo, vos no tenés nada que ver) no decía exactamente lo mismo que el enunciado. ¿Te acordás? ¿A qué me refería? |
|
|
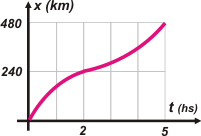 |
|
Bien: el enunciado dice que el móvil recorre 240 kilómetros... y después otros 240 más... pero no dice que los recorre a velocidad constante... como representan esas gráficas rosas.
Bien podría haber recorrido a velocidades cambiantes un poco más despacio, después más rápido, libremente... hacer lo que se le da la gana... |
|
|
|
| O sea, había miles, millones, infinitos gráficos posibles para este enunciado. Acá te hice uno sólo de esos infinitos... uno que se me ocurrió. |
|
|
| |
|
 |
| DESAFIO: Hacete tres gráficos más de movimientos posibles... (con un poco más de onda que el mío que fue bastante aburrido). Y uno imposible. |
|
| |
|
| Algunos derechos reservados.
Se permite su reproducción citando la fuente. Última actualización ago-10. Buenos Aires, Argentina. |
|
|
| | |
|
|

