NO ME SALEN
PROBLEMAS RESUELTOS DE BIOFÍSICA DEL CBC
(Movimiento uniforme)
|
|

|
| |

|
5) ¿A qué hora debe pasar un automovilista por la localidad A, a una velocidad constante de 80 km/h, si desea alcanzar a las 13 horas a otro automovilista que pasó por el mismo lugar a las 8 horas y que mantiene una velocidad constante de 40 km/h? |
Se trata de un sencillo problema de persecución y encuentro. Reconozco que el enunciado tiene una estructura un tanto rebuscada; pero leelo despacio, no es difícil.
El auto más lento (que voy a llamar 1) pasa por A a las 8 de la mañana. Más tarde, no sé a qué hora, pasa el otro, que es más veloz (y que voy a llamar 2), con la idea de alcanzarlo justo a las 13 vaya uno a saber dónde. Mirá este gráfico a ver si te cierra. | |
|
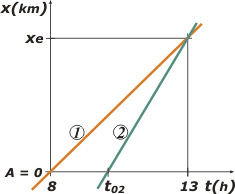 |
Puse el cero de las posiciones en la ciudad A, ya que todo lo que ocurra del otro lado de la ciudad no nos interesa.
Eso sí, las rectas que representan los movimientos de los autos (naranja el que va a 40 y verde el que persigue a 80) las dibujé "cruzando" el cero... para respetar el enunciado, que dice pasan por A (y no: parten de A).
El instante en el que el perseguidor pasa por A, que desconozco, lo llamé t02, y la posición en la que se encuentran, xe. Espero que estés de acuerdo. |
|
|
|
Ahora tengamos a mano el modelo de ecuación horaria que vamos a usar:
x = xo + v ( t – to )
Para armar las ecuaciones de los autos necesito tres constantes de cada uno: la velocidad, una posición (voy a tomar el cero) y el instante de tiempo que se corresponde. Quedan así: |
|
|
| auto 1 |
x = 40 km/h ( t – 8 h)
|
Abajo hay otro recuadrito amarillo en el que te hago un comentario sobre estas ecuaciones |
| auto 2 |
x = 80 km/h ( t – t02)
|
|
|
|
| A estas dos ecuaciones que describen -cada una- totalmente el movimiento de cada auto, les vamos a pedir que hablen exclusivamente de la posición y el instante de encuentro. Fijate: |
|
|
 |
xe = 40 km/h ( 13 h – 8 h)
|
[1] |
xe = 80 km/h ( 13 h – t02)
|
[2] |
|
|
|
inevitablemente desembocás en un sistema de dos ecuaciones con dos incógnitas. Acá terminó la física del problema. Lo que queda es álgebra y hay 312 caminos diferentes para resolverlo. Espero que te animes solo.
En la [1] calculo xe
xe = 200 km
Con ese valor voy a la ecuación [2] y despejo t02 |
|
|
|
|
|
| Comentario: esas dos ecuaciones (funciones) nadie las escribe. Ningún libro con ejercicios resueltos, ningún apunte de ejercicios resueltos, ningún profesor en su clase, ningún estudiante en su práctica ni en su examen... Todos las saltean y van directamente a las dos que siguen, que yo llamé [1] y [2], ¡y son la parte más substanciosa de la física! ¡Son las expresiones que describen todo el movimiento, todo el fenómeno natural! ¡Como profesional de la salud NUNCA vas a tener que calcular encuentros de automóviles! En cambio... vas a tener que enfrentar fenómenos naturales que se DESCRIBEN con funciones como las que tenés ahí. Llevate eso; la cinemática es sólo una excusa. |
|
|
|
| |
|
 |
| |
|
| DESAFIO: Rehacé el problema pero tomando instante de tiempo inicial (pasaje por A) a la hora 0. Es común hacer eso, pero hay que interpretar el resultado y corregirlo. |
|
| |
|
Algunos derechos reservados.
Se permite su reproducción citando la fuente. Última actualización ago-07. Buenos Aires, Argentina.
|
|
| | |
|
|

