NO ME SALEN
APUNTES TEÓRICOS Y EJERCICIOS RESUELTOS DE FÍSICA DEL CBC

|
|

|
| SUMA ANALITICA DE VECTORES
En las páginas anteriores llegamos a la conclusión de que un buen método para expresar analíticamente un vector es la siguiente:
V = Vx î + Vy ĵ
donde V es el vector que queda expresado en la forma analítica; Vx y Vy son las coordenadas de los ejes x e y respectivamente; î y ĵ son los versores en cada eje. |
 |
Inventemos un ejemplo: los vectores A y B se expresarán de esta manera:
A = 7 î + 2 ĵ
B = î + 4 ĵ
|
|
|
|
| Expresados de esta manera, hallar el vector suma de A y B es muy sencillo. |
|
|
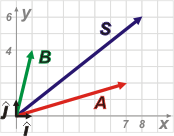 |
Basta con sumar los segundos miembros componente a componente:
S = 8 î + 6 ĵ
Ya que (7 î + î = 8 î ) y (2 ĵ + 4 ĵ = 6 ĵ ). |
|
|
|
La explicación de esto es muy sencilla, y podés encararla por dos caminos. Para que los entiendas más fácil dibujé uno de los vectores, el B, a continuación del otro. |
|
|
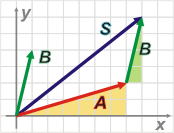 |
Así se ve, claramente, que S es la suma de A y B. Además dibujé dos triangulitos debajo de cada vector que se suma, para que tengas en cuenta los catetos, que no son otros que las descomposiciones, las proyecciones x e y de cada vector.
Si tenemos éxito, entonces, te habrás dado cuenta de que la componente x del vector suma es igual a la suma de los componentes x de cada vector que se suma. Y lo mismo para las componentes y. ¿Te cerró? |
|
|
|
RESTA DE VECTORES (GEOMÉTRICA Y ANALÍTICAMENTE)
Si ya dominás analítica y geométricamente la suma de vectores, hacer la resta es bien sencillo, ya que restar M y S (elegí esos nombres por minuendo y sustraendo) es lo mismo que sumar M y –S:
M – S = M + (–S)
De modo que basta con multiplicar por -1 a un vector (o sea, invertirlo) para fabricar una resta a partir de una suma.
Sin embargo, como la resta entre vectores tiene una importancia especial, vamos a desarrollarla completamente y a destacar algunas propiedades importantes.
La principal es que la resta (tanto de los vectores como de los escalares) no es conmutativa. Para todo el mundo es fácil comprender que 5 – 3 no es lo mismo que 3 – 5. No es tan obvio con los vectores, pero es así: |
|
|
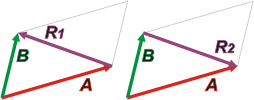 |
Una diagonal del paralelogramo que se forma con dos vectores cualesquiera se corresponde con la resta de los vectores. La resta no es conmutativa, con los vectores tampoco:
B – A = R1
A – B = R2
|
|
|
|
Probemos analíticamente el segundo caso:
A = Axî + Ay ĵ = 7 î + 2 ĵ
B = Bxî + By ĵ = î + 4 ĵ
|
|
|
 |
(Son los mismo que usé antes). |
|
|
|
Ahora restamos:
A – B = R2
A – B = ( 7 î + 2 ĵ ) – ( î + 4 ĵ )
A – B = 7 î + 2 ĵ – î – 4 ĵ
A – B = 6 î – 2 ĵ = R2
|
|
|
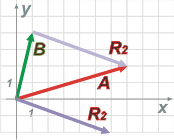 |
Y, como ves, su representación centrada en el origen es equivalente al vector que une los extremos de los vectores que se restan, con origen en el sustraendo y extremo en el minuendo.
Cuando los vectores que tengas que restar representen situaciones anteriores y posteriores (inicial y final) el sentido de la resta (si es R1 o R2) va cobrar sentido automáticamente. |
|
|
|
| |
|
|
| CHISMES IMPORTANTES: |
|
|
- En mis clases postergo todo lo que puedo la enseñanza del álgebra vectorial hasta que se torna imprescindible. Pese a que los físicos afirman que la cinemática y la dinámica son totalmente vectoriales (y tienen razón), yo opino que se puede hacer una cinemática muy rica y útil sin necesidad de vectores, y que la vectorialización temprana es un estorbo muchas veces desmoralizador.
|
|
 |
| ir derecho a la siguiente de vectores |
| Algunos derechos reservados.
Se permite su reproducción citando la fuente. Última actualización nov-09. Buenos Aires, Argentina. |
|
|
|

