 |
NO ME SALEN
APUNTES TEORICOS DE FÍSICA Y BIOFÍSICA DEL CBC
|
|

|
Aceleración
La aceleración no es tan intuitiva. Pero muchas personas la interpretan correctamente de entrada y la asocian con presteza con vivencias propias. Se trata de la magnitud que describe el cambio de velocidad.
Si necesitamos ponerle fórmulas no es tan sencillo pero podemos hacer el mismo derrotero que hicimos para definir la velocidad, y vuelve a ser apasionante. Vamos a hacerlo de a poco, en etapas.
Aceleración media
En un primer paso podríamos decir que la aceleraciónes el cociente entre un cambio de velocidad (una diferencia entre velocidades), y el tiempo insumido en ese cambio. En una fórmula: |
|
| a |
= |
Δv12 |
= |
v2 – v1 |
|
|
|
| Δt12 |
t2 – t1 |
|
|
donde v1 y v2 representan las diferentes velocidades y t1 y t2 los instantes de tiempo correspondientes a cada velocidad.
Esa definición tiene una debilidad importante. Si uno calcula una aceleración de ese modo no puede asegurar que la aceleración no haya variado durante ese intervalo, mientras ocurre el cambio de velocidad. Podríamos decir que ese modo de formular la aceleración es una especie de promedio de las aceleraciones reales que tiene un móvil en cada momento. Entonces a la formulación anterior la llamaremos aceleración media, y la simbolizamos am. El único caso en que la aceleracion media es la aceleración real de un móvil es cuando éste se desplaza sin cambiar su aceleración, o sea, en el movimiento rectilíneo uniformemente variado, MRUV.
Hagamos un alto. Porque ya que estamos acá podemos analizar cuáles son las unidades en las que habremos de medir las aceleraciones. Obviamente deberán corresponderse con el cociente entre una unidad de velocidad y una unidad de tiempo. En el sistema internacional de medidas ellas son el metro, m/s, y el segundo, s. |
|
|
|
Aunque no es la única es la más cómoda y es muy raro que se usen otras.
Velocidad instantánea
Bueno, sigamos afinando la formulación de velocidad. Hasta ahora tenemos: |
|
|
|
|
|
Y ya estás advertido que esa definición no representa la aceleración de un móvil instante por instante sino una especie de promedio en un cierto lapso, y que no describe lo que pasa durante el lapso.
A esa aceleración real del móvil en cada instante la llamaremos (para distinguirla de la media) aceleración real o aceleración instantánea. Y podemos acercarnos (cuanto querramos) al concepto buscado tomando variaciones de velocidad (o intervalos de tiempo) muy pequeños.
El análisis matemático propone una solución a este problema de tomar intervalos súper pequeños. Se trata de la operación límite, y básicamente dice que se puede operar con intervalos tan, pero tan pequeños que son casi nulos. En la jerga matemática: infinitésimos. La formulación es la que sigue: |
|
|
|
|
|
Comparala con la formulación de la velocidad media, notarás que lo único que cambia es que tanto el desplazamiento como el intervalo de tiempo considerados son infinitamente pequeños.
Estas cantidades infinitesimales se llaman diferenciales y se las simboliza con una d minúscula. Entonces: |
|
|
| a |
= |
lím |
|
Δv |
= |
dv |
|
|
| Δt →0 |
|
|
| Δt |
dt |
|
|
|
Ahora sí, disponemos de una definición exacta y sin ambigüedades de aceleración. Pero ya que estamos acá aprovechemos la oportunidad para observar algunas propiedades deslumbrantes de esta magnitud y del modo en que la definimos. |
|
|
 |
|
|
Derivada
Si sabés algo de análisis matemático (si no, no importa, yo te lo cuento) la definición de arriba (el límite tendiendo a cero del cociente incremental) no es otra cosa que la derivada. De donde podemos concluir que la aceleración es el derivada de la función velocidad (o, sencillamente: la aceleración es la derivada de la velocidad). En símbolos:
a = v'
De modo que la aceleración es la magnitud que describe los cambios de la velocidad, te dice si las velocidades cambian rápidamente o lentamente o no cambian. ¡Y eso es, justamente, lo que entendemos coloquialmente por aceleración!
Pero también habíamos visto que la velocidad era la derivada de la posición. De modo que la aceleración es la derivada segunda de la posición:
a = v' = x''
Signo de la aceleración
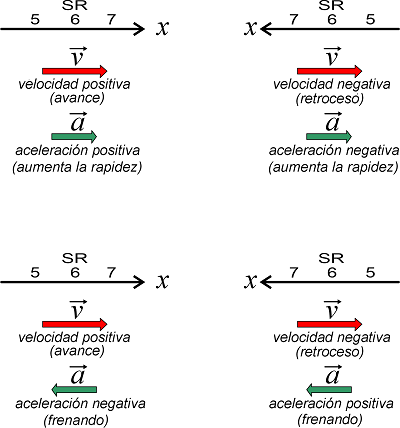
El signo de la aceleración no indica si el móvil está frenando o aumentando la rapidez. Cuando un móvil disminuye su rapidez (el módulo de su velocidad) suele decirse que el movimiento es desacelerado, pero eso no implica que su aceleración sea negativa.
En signo de la aceleración depende exclusivamente del sistema de referencia. Acá tenés un cuadro explicativo que contempla todas las posibilidades. |
|
|
 |
|
|
La representación vectorial es acá muy descritiva.
Perplejidades
Pero hay algo más importante: fijate que cuando el intervalo de tiempo tiende a cero el cambio de velocidad también tiende a cero. O sea que el cociente dv/dt es del tipo 0/0. Tal como lo discutimos con la velocidad, esos límites podrían no existir, ser indeterminados. Sin embargo en nuestro universo ese límite siempre existe, siempre arroja como resultado un número real, cosa que se verifica experimentalmente.
Y eso nos está diciendo algo muy relevante: ¡la función cuya derivada siempre existe debe ser una función continua y derivable! ¡Y eso es, efectivamente, lo que ocurre en nuestro universo! Dicho de otro modo: la función que describe la velocidad no tiene baches y no pega saltos. Ningún móvil puede dejar de tener una velocidad y si pasa de una velocidad a otra diferente el universo lo obliga a pasar por las infinitas velocidades intermedias.
Derivadas sucesivas - Tirón
Vimos que derivando sucesivamente la función que describe la posición obtenemos la velocidad (primera derivada) y la aceleración (segunda derivada). ¿Se puede seguir derivando? ¿Tiene sentido? Sí, obviamente se puede seguir derivando, pero va perdiendo sentido rápidamente.
La derivada de la aceleración tiene nombre propio, el tirón (jerk en la literatura anglosajona), que se simboliza j. Y su interés es relativo: ya vas a ver en dinámica que una función que describe cómo varía la aceleración es útil para estudiar cómo varían las fuerzas.
Pero esa derivada no siempre existe, lo que significa que la aceleración puede no ser continua y pegar saltos. Lo mismo le pasa a las siguientes derivadas sucesivas, que describen poco o nada del funcionamiento del universo. |
|
|
|
|
|
CHISMES IMPORTANTES: |
|
|
- El término perplejidades (cosas que te dejan perplejo) se lo debemos a Eduardo Flichman (1932-2005) físico y filósofo de la ciencia argentino que trabajó muchos años en el CBC de la Universidad de Buenos Aires.
- El inventor del análisis matemático fue Isaac Newton (junto con Gottfried Leibniz) que la desarrolló pensando, justamente, en cuestiones cinemáticas: posición, velocidad, aceleración.
|
|
|
| PREGUNTAS CAPCIOSAS: |
|
|
- Observando el movimiento de un cuerpo, ¿es posible decidir si tiene una aceleración positiva o negativa?
|
|
 |
| |
|
| |
|
| | |
|
| Algunos derechos reservados.
Se permite su reproducción citando la fuente. Última actualización ago-23. Buenos Aires, Argentina. |
|
|
 |
| | |
|
|
|

