 |
NO ME SALEN
(EJERCICIOS RESUELTOS Y APUNTES TEÓRICOS DE FÍSICA)
TRIGONOMETRÍA
|
|

|
| |
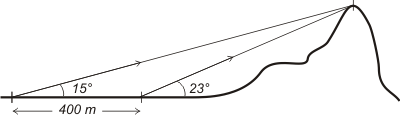
EJERCICIO 1 - Se desea conocer la altura de un cerro. Si se mira su cima desde cierta distancia, el ángulo con el que hay que mirarlo es de 15 grados (respecto a la horizontal). 400 metros horizontales más cerca, el ángulo es de 23 grados. ¿Cuál es la altura del cerro?
|
| |
 |
|
|
Este ejercicio nos muestra qué útil es la trigonometría como herramienta de cálculo. Fijate que no sabemos a qué distancia del cerro estamos, ni menos aún a qué distancia de la vertical que pasa por la cima... si lo supiéramos el ejercicio sería mucho más fácil. Pero esas distancias casi nunca se conocen.
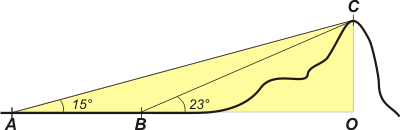
Fijate el triángulo rectángulo imaginario que trazamos acá: |
|
|
 |
|
|
De paso le puse nombre a los puntos notables. En A y en B (distantes 400 m entre sí) es donde se tomaron las mediciones de los ángulos. C es la cima. O es el punto sobre la horizontal que está justo abajo de la cima. Luego CO es la altura que deseamos conocer.
En el triángulo ACO, que es rectángulo, AO es el cateto adyacente al ángulo de 15°, y CO es el cateto opuesto. Entonces podemos escribir:
CO = AO . tg 15°
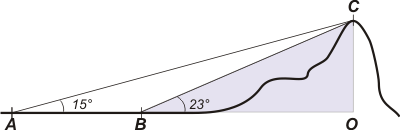
Si ahora mirás este otro triángulo: |
|
|
|
|
|
Admitirás que:
CO = BO . tg 23°
Ya tenemos dos ecuaciones. Pero hay una tercera:
AO — BO = 400 m
Y si te fijás, tenemos sólo tres incógnitas. O sea... ya está, el resto es álgebra. Y no llores, yo te lo hago.
Voy a meter las dos primeras (las de trigonometría) en la tercera: |
|
|
| |
CO |
— |
CO |
= 400 m |
|
|
|
| tg 15° |
tg 23° |
|
|
|
| Y ya alcanza con despejar CO y calcular: |
|
|
| |
CO = 400 m |
tg 23° . tg 15° |
|
|
|
| tg 23°— tg 15° |
|
|
|
|
|
|
| Con esto ya te recibiste de topógrafo. Estos profesionales que miden -entre otras cosas- las diferencias de nivel en el terreno, usan un instrumento clave en el oficio, el teodolito. |
|
|
 |
|
El método que desarrollamos en este ejercicio es muy preciso. Las mediciones clave son las de los ángulos, que son las que se realizan con el teodolito, y que pueden resolverse en segundos de grado. Por supuesto, también hay que tener precisión en la distancia entre las dos mediciones, y del hecho de que se hagan al mismo nivel. Por último, habrá que sumar la altura del mismo instrumento.
Qué más querés. |
|
|
|
| DESAFIO: ¿Te animás a resolverlo usando la cotangente en lugar de la tangente? |
|
 |
| |
|
| |
|
| Algunos derechos reservados. Algunos izquierdos también. O sea: propiedad intelectual, propiedad vertical, propiedad horizontal y la propiedad del prójimo. Se permite su reproducción citando la fuente, o sea a mí. Última actualización may-21. Buenos Aires, Argentina. |
|
|
| | |
|
|

