 |
NO ME SALEN
(EJERCICIOS RESUELTOS Y APUNTES TEÓRICOS DE FÍSICA)
Funciones
|
|

|
| |
FIS a1.13- Hallar todas las soluciones reales de las
siguientes ecuaciones y verificar, cuando corresponda,
el resultado obtenido.
a) x² — 9 = 0
b) 5x² — 2x = 0
c) (x + 3)² — 4 = 0
d) (x — 2)² + 1 = 0
e) 3x² = 4 — x
f) 6x² + 21x = 12
|
| |
Muchas veces nos sentimos tentados a resolver estos ejercicios algebraicamente (cosa que se puede hacer cuando la ecuación es incompleta, o sea, cuando no tiene término lineal o independiente), pero más de una vez caemos en la trampa siguiente: nos olvidamos que la raíz cuadrada admite dos soluciones (por ejemplo la raíz de 9 es tanto 3 como -3) y otras veces olvidamos las soluciones triviales. Te voy a ir mostrando los momentos en que solemos equivocarnos, para que te vayas acostumbrando.
En cambio, si somos pacientes, escribimos la ecuación en su forma canónica:
ax² + bx + c = 0
y aplicamos la ecuación salvadora que descubrieron los griegos: |
|
|
| |
x1 , x2 = |
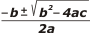 |
|
|
|
Y ahí no hay mucha posibilidad de equivocarse. De modo que las ecuaciones incompletas las voy a resolver algebraicamente para que pesques la idea.
a) Incompleta, no tiene término lineal, b = 0.
x² — 9 = 0
x² = 9 (OJO: esto admite dos soluciones)
|
|
|
|
|
|
b) Incompleta, no tiene término independiente, c = 0.
5x² — 2x = 0
5x² = 2x (OJO: si x vale 0 la igualdad se satisface)
5x = 2
x = 2/5
|
|
|
|
|
|
c) Completa, operamos algebraicamente para encontrar la ecuación completa y visualizar los coeficientes.
(x + 3)² — 4 = 0
x² + 6x + 9 — 4 = 0
x² + 6x + 5 = 0
Ahora sí: a = 1, b = 6, c = 5. Aplicamos la resolvente. |
|
|
|
|
|
d) Completa, lo mismo que la anterior.
(x — 2)² + 1 = 0
x² — 4x + 4 + 1 = 0
x² — 4x + 5 = 0
Ahora sí: a = 1, b = — 4, c = 5. Aplicamos la resolvente. Y encontramos que no tiene solución porque el discriminante es negativo. |
|
|
|
|
|
e) Completa, acomodemos la ecuación:
3x² = 4 — x
3x² + x — 4 = 0
Ahora sí: a = 3, b = 1, c = — 4. Aplicamos la resolvente. |
|
|
| |
x1 = — 1,33... ; x2 = 1 |
e) |
|
|
|
f) Completa, acomodemos la ecuación:
6x² + 21x = 12
6x² + 21x — 12 = 0
Ahora sí: a = 6, b = 21, c = — 12. Aplicamos la resolvente. |
|
|
|
|
|
| En la actualidad existen aplicaciones tanto de computadora como de celular que resuelven cuadráticas y funciones más complicadas en menos de un segundo y sin equivocarse. Andá procurándote la tuya y aprendé a usarla. También las hay que grafican con mucha precisión, son excelentes herramientas. |
|
|
| |
|
|
| DESAFIO: Transformá las ecuaciones en funciones y graficalas. Interpretá en esos gráficos las soluciones que encontramos en este ejercicio. |
|
 |
| |
|
| |
|
| Algunos derechos reservados.
Se permite su reproducción citando la fuente. Última actualización mar-16. Buenos Aires, Argentina. |
|
|
| | |
|
|

