 |
NO ME SALEN
(EJERCICIOS RESUELTOS Y APUNTES TEÓRICOS DE FÍSICA)
Funciones
|
|

|
| |
FIS a1.12 - Sabiendo que la abscisa del vértice es el punto
medio entre las dos raíces de la función, verificar
que:
xV = — b / (2a)
yV = — (b² — 4ac) / (4a)
|
| |
Es inusual en No me salen un ejercicio teórico, como éste. Vamos a tomarlo como un simple ejercicio de álgebra.
Dice el enunciado que la abcisa del vértice(o sea, la coordenada xV ) es el punto medio de las raíces, x1 y x2. Y recordando que el punto medio se halla sumando las coordenadas y dividiendo por dos:
xV = ½ ( x1 + x2 )
Bien, pero cada raíz la podemos encontrar utilizando los coeficientes de la ecuación, con la famosa: |
|
|
| |
x1 , x2 = |
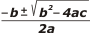 |
|
|
|
| Una raíz usando la suma y la otra usando la resta. Si sumamos ambas una la ponemos restando y la otra sumando: |
|
|
| xV = |
½ ( |
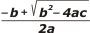 |
+ |
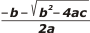 |
) |
|
|
|
| Las dos fracciones tienen el mismo divisor y se pueden juntar, y de paso lo multiplicamos por el 2 del un medio. |
|
|
| xV = |
|
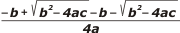 |
|
|
|
|
|
| Las raíces cuadradas son idénticas y aparecen sumando y restando, o sea, se cancelan. Y b aparece restando dos veces, ese 2 se simplifica con el 4 de abajo... |
|
|
|
|
|
Que es lo que queríamos demostrar. Pero todavía nos falta la ordenada del vértice, yV. para hallarla recurrimos al modelo de ecuación de la parábola, expresada para el vértice.
yV = a xV² + b xV + c
Lo usual... pero hablando del vértice. Y en ella reemplazamos xV por lo que tenemos del paso anterior. |
|
|
| yV = a ( |
— b |
)² + b ( |
— b |
) + c |
|
|
| 2a |
2a |
|
|
|
| No te pierdas... |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
| Queda entonces demostrado por los siglos de los siglos. |
|
|
| DESAFIO: usá estas fórmulas para ponerlas a prueba con una parábola cualquiera que ya tengas graficada. |
|
 |
| |
|
| |
|
| Algunos derechos reservados.
Se permite su reproducción citando la fuente. Las abcisas andan por el suelo. Última actualización mar-16. Buenos Aires, Argentina. |
|
|
| | |
|
|

