FIS a1.02- Determinar la pendiente y la ordenada al origen de las siguientes funciones:

Acordate que se llama función lineal (o también función polinómica de primer grado) a la función de la forma:

f_(x) = a x + b

Donde a y b son dos números reales que representan la pendiente (o inclinación de la gráfica) y la ordenada al origen (o término independiente, que es el valor de la función para x = 0) respectivamente.

a) f_(x) = 3. Se trata, efectivamente de una función lineal. La pendiente vale 0 y la ordenada al origen también. a = 0 y b = 3.

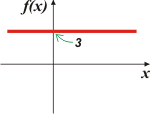Su representación gráfica es ésta. Cuando la pendiente vale cero, como en este caso, nos encontramos con un subgrupo de las funciones lineales: la función constante.

Interpretalo de esta manera: para cualquier valor de x (fijate que no figura en la función, el valor de esta es 3.

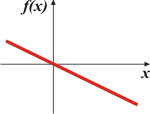En cuanto a la inclinación (o pendiente), fijate que el gráfico que elegí no tiene las mismas escalas en ambos ejes. Si hubiese elegido uno cuyos ejes hubieran tenido la misma escala, la curva también sería decreciente, pero mucho más empinada.

c) f_(x) = 4 — 1/5 x. Bueno, esto ya se pone un poco pesado... A ver...

Acá a = — 1/5. O si preferís, a = — 0,2. Y b = 4. Te lo escriben en orden invertido para que recuerdes de el orden de los términos no altera la suma.

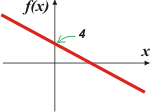Notarás, acá también, que los ejes no llevan la misma escala: la recta corta al eje de las x en el 20.

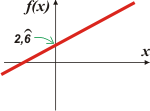
d) f_(x) = (5x + 8)/3. Qué pesados... Empecemos por distribuir ese 3 del denominador entre ambos términos del numerador. La ecuación queda así:

f_(x) = 1,67 x + 2,67

Redondeando un poco. También la podría escribir en forma exacta usando fracciones.