 |
NO ME SALEN
(EJERCICIOS RESUELTOS Y APUNTES TEÓRICOS DE FÍSICA)
Funciones
|
|

|
| |
FIS a1.01- Indicar cuáles de las siguientes funciones
son lineales.
a) f(x) = 0
b) f(x) = 2x + 3
c) f(x) = — 1/3 x
d) f(x) = 5x² — x
e) f(x) = (x — 1)² + 3x
f) f(x) = 2x + 3; para x ≤ 0 y f(x) = 3; para x > 0
|
| |
Acordate que se llama función lineal (o también función polinómica de primer grado) a la función de la forma:
f(x) = a x + b
Donde a y b son dos números reales que representan la pendiente (o inclinación de la gráfica) y la ordenada al origen (o término independiente, que es el valor de la función para x = 0) respectivamente.
La representación gráfica de una función lineal es siempre una recta no vertical. |
|
|
a) f(x) = 0. Aunque elude la definición estricta de función lineal (función polinómica de grado 1), amigablemente la admitimos en el club de las lineales. Su pendiente vale 0 y la ordenada al origen también. a = 0 y b = 0. |
|
|
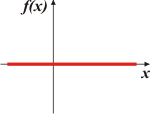 |
Su representación gráfica es ésta. Cuando la pendiente vale cero, como en este caso, nos encontramos con un subgrupo de las funciones lineales: la función constante.
Si el valor de la ordenada al origen fuese distinto de 0, las gráficas correspondientes igualmente sería paralelas al exe x, pero más arriba (b>0) o más abajo (b<0). |
|
|
| b) f(x) = 2x + 3. Obvio que sí. a = 2 y b = 3. Caso típico. Mirá el gráfico. Ahí se ve claramente que la ordenada al origen es el valor de la función cuando la variable independiente es nula. |
|
|
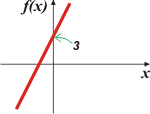 |
En cuanto a la inclinación (o pendiente), de la gráfica, si la función es de nímeros reales, o sea, que podríamos representarla así:
y = 2x + 3
entonces conviene que las escalas de los ejes sean idénticas. En ese caso la pendiente te indica cuántas unidades de la función (y) aumenta o disminuyen cada cuántas unidades de la variable independiente (x). |
|
|
En nuestro gráfico... mirá el triangulito que se forma entre la curva y los ejes. Su altura vale 3, luego la base debe medir 1,5, ya que a = Δy/Δx, a = 3 / 1,5, a = 2.
Pero si la función fuese real pero no numérica (por ejemplo presión de un fluido en función de la profundidad), o si por el motivo que fuese tenemos una representación gráfica cuyos ejes tienen escalas diferentes, entonces, la inclinación de la gráfica no se debe interpretar geométricamente. |
|
|
| c) f(x) = — 1/3 x. Claro que sí, que se trata de una función lineal. Acá a = — 0,33... y b = 0. |
|
|
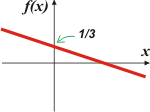 |
Veamos el gráfico. ¿Llegás a darte cuenta si los ejes tienen la misma escala? La respuesta es sí, la misma escala.
También podés observar que si a, la pendiente, es negativa, la gráfica es descendente. |
|
|
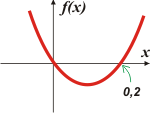
| d) f(x) = 5x² — x. Esta función no es lineal, de acá a la China. Cuando la variable independiente, en este caso x, aparece al menos una vez elevada al cuadrado o a cualquier potencia distinta de 1 (que es cuando la potencia no se escribe) la función deja de ser lineal y se convierte en una función potencial; en este caso de grado 2, o cuadrática. |
|
|
|
La forma de la gráfica es típica, se trata de una parábola. Con la práctica vas a poder dibujarla a mano alzada (que es lo deseable) y predecir es va para arriba, para abajo, más abierta, más cerrada, más corrida a la izquierda o a la derecha, o perfectamente centrada. Por ahora podés fijarte que si el término independiente u ordenada al origen vale cero... la gráfica deberá cortar el origen de los ejes. |
|
|
| e) f(x) = (x — 1)² + 3x. De acá a la china otra cuadrática. Pero tal vez no te resulte tan fácil de interpretar como la anterior. trata de llevarla (operando algebraicamente) a la forma tradicional: f(x) = ax² + bx + c. Donde a, b y c son los coeficiente cuadrático, coeficiente lineal y término independiente respectivamente. O sea que los que en la cuadrática llamamos b, en la lineal llamamos a; y lo que en la cuadrática llamamos c, en la lineal b. |
|
|
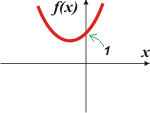 |
No es difícil, hacelo vos y llegá a lo mismo que yo:
f(x) = x² + x + 1
Y mirá el gráfico. |
|
|
| f) f(x) = 2x + 3; para x ≤ 0 y f(x) = 3; para x > 0 |
|
|
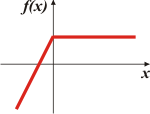 |
Bueno... ahí la tenés. Con ella podés divertirte un rato largo discutiendo con tus docentes en clase y tratando de responder la pregunta del enunciado. |
|
|
| Desafío: ¿Te animás a decirme en qué valor de x tiene su vértice la parábola de la función d)? |
|
 |
| |
|
| |
|
| Algunos derechos reservados.
Se permite su reproducción citando la fuente. Última actualización mar-16. Buenos Aires, Argentina. |
|
|
| | |
|
|

