 |
NO ME SALEN
(EJERCICIOS RESUELTOS Y APUNTES TEÓRICOS DE FÍSICA)
Funciones
|
|

|
| |
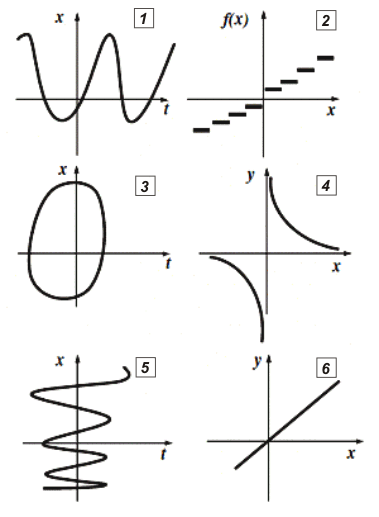
FIS a1.00- Indicar cuáles de los siguientes gráficos
representa una función en el conjunto R de los
números reales.
|
| |
 |
|
|
La clave de este ejercicio consiste en verificar que exista un solo valor de f(x) para cada valor de x o de t, según el caso. |
|
|
1. Este gáfico representa una función sin lugar a dudas. Esa función se puede representar así: x(t). Y así la vas a encontrar escrita por todos lados, aunque la notación correcta es así: x(t), con el paréntesis (t) escrito como subíndice. De no ser así, la notación multiplicación y la notación variable independiente serían indistinguibles. Pero la costumbre puede más que la norma, y la distinción la hacemos por el contexto. (Prometo que no vuelvo a hacer este comentario). |
|
|
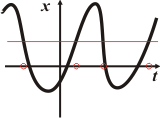 |
La única dificultad que te puede presentar la interpretación de esa función surge del hecho de que hay varios valores de t para los que la función, x, vale lo mismo. Basta con que traces una recta paralela al eje de las t (lo hice en rojo) para que encuentres cuatro valores de t (los marqué con circulitos rojos) para los que la función vale lo mismo.
Pero eso no hace que deje de ser función. |
|
|
| 2. Este gráfico también puede ser una función, f(x). Claro, hay detalles que el gráfico no permite establecer a ciencia cierta, por una cuestión de escala. Pero en principio no podemos objetarla. Hay dos dificultades. La primera son esos saltos. Bien, los saltos están permitidos, que haya saltos no quiere decir que no sea función. Lo que se puede decir es que la función no es derivable en los bordes del salto. |
|
|
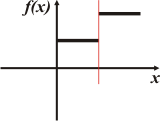 |
Pero los saltos tienen sus condiciones. Acá te hice la ampliación de un salto. Fijate: el salto debe ser tal que no exista ningún valor de la variable independiente (en este caso, x) para el que no haya valor de f(x). O sea, el conjunto de partida debe estar totalmente cubierto. Y la segunda condición es que no puede caber duda de cuál de los dos valores de f(x)es el que corresponde al valor de x en el que se produce el salto, debe ser uno y sólo uno. |
|
|
| Espero que resuelvas el desafío (que se refiere a este gráfico) y explores cómo se cumplen las condiciones que acabo de exponer. |
|
|
| 3. Este gráfico, no cabe duda, no representa una función x(t). Basta con que traces una recta paralela al eje x, para ver que al valor de t (la variable independiente, flechita verde) le corresponden dos valores de x (te los marqué con circulitos). |
|
|
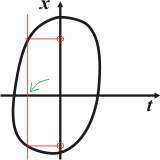 |
Hay infinitos valores de t para los que la gráfica da dos valores, en este gráfico te mostré apenas uno. De modo que esto no puede ser gráfico de una función.
Puestos a salvarlo... podríamos "cortar" cuidadosamente esa especie de huevo de dinosaurio sarnoso en dos mitades, una superior y otra inferior, de modo de que el gráfico se convierta en la representación de dos funciones. ¿Te animás a hacer el corte? En la gráfica salvada, habría que ponerle colores diferentes a las dos funciones. |
|
|
| 4. Este gráfico sí puede representar una función, y(x), y hay varios ejemplos de funciones notables que tienen una pinta parecida, entre ellas la función y = 1/x. Pero claro, hay un valor de x conflictivo. En mi ejemplo cuando x = 0 el valor de la función no existe. Estrictamente esto hace que la función no sea tal. Pero al tratarse de una singularidad podemos salvarla de alguna manera y admitirla entre el club de las funciones. Por ejemplo podríamos salvarla así "sea la función y = 1/x definida en todos los reales menos el 0..." y ya. |
|
|
5. Este gráfico no puede representar una función. x(t), en este caso no es función. Aunque sí podría ser una función t(x) (su inversa), pero claro, no se representaría de esa manera.
6. Este gráfico representa la función más famosa del universo, la función lineal; particularmente, la función identidad y = x. |
|
|
| No es por capricho que las funciones matemáticas tengan estas restricciones y condiciones que cumplir, por ejemplo, la distinción entre variable independiente y variable dependiente, que es la función propiamente dicha. Todos los fenómenos naturales matematizables, de cualquier rama de la ciencia que se te antoje, se describen con funciones reales. La palabra real, termina aludiendo a que puede describir la realidad. Qué me contás. |
|
|
| Desafío: ¿A qué función notable se parece mucho el gráfico 2? |
|
 |
| |
|
| |
|
| Algunos derechos reservados.
Se permite su reproducción citando la fuente. Última actualización mar-16. Buenos Aires, Argentina. |
|
|
| | |
|
|

