 |
NO ME SALEN
(EJERCICIOS RESUELTOS Y APUNTES TEÓRICOS DE FÍSICA)
Funciones derivadas
|
|

|
| |
FIS a2.13 - Debido a unas pésimas condiciones
ambientales, una colonia de un millón de bacterias
no comienza su reproducción hasta pasados
dos meses. La función, f(t), que representa la
población de la colonia al variar el tiempo
(expresado en meses) viene dada por:
|
| |
| f(t) = |
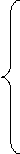 |
106 |
si 0 < t < 2 |
| 106. e(t-2) |
si t ≥ 2 |
|
|
|
a) Calcular la tasa de variación media de la
población en los intervalos [0 ; 2] y [0 ; 4].
b) Calcular la tasa de variación instantánea en
t = 4.
|
|
|
Qué placer, un ejercicio especial para biólogos. Vamos juntos sin temor a infectarnos.
Cuando nos piden la tasa de variación (nombre elegante) no es otra cosa que la velocidad de crecimiento, que es derivada respecto al tiempo de la función número de bacterias, o sea la población (la función del enunciado). De modo que podemos llamarla f'(t). Esto nos va a servir sólo para la pregunta b).
Porque en cambio la tasa de variación media (voy a simbolizarla así: f'm(t1 ; t2)) es algo así como el promedio entre dos instantes respecto al tiempo Cuánto había entonces, cuánto hay ahora, con qué velocidad creció en promedio: |
|
|
| f'm(t1 ; t2) = |
|
f(t2) — f(t1) |
|
|
|
| t2 — t1 |
|
|
|
| Hagamos los cálculos para el período [0 ; 2]. |
|
|
| f'm(0 ; 2) = |
|
f(2) — f(0) |
|
|
|
| 2 —0 |
|
|
|
|
|
|
|
|
|
| Ahora el período [0 ; 4] |
|
|
| f'm(0 ; 4) = |
|
f(4) — f(0) |
|
|
|
| 4 —0 |
|
|
|
| f'm(0 ; 4) = |
|
106. e2 — 106 |
|
|
|
| 4 |
|
|
|
|
|
|
Ahora sí, vamos a la velocidad instantánea, y nos ponemos a derivar. En realidad son dos funciones y sus derivadas también serán dos funciones. Acordate que la derivada de una constante vale 0 y que la derivada de la funcion exponencial es igual a su primitiva. |
|
|
| f'(t) = |
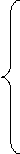 |
0 |
si 0 < t < 2 |
| 106. e(t - 2) |
si t ≥ 2 |
|
|
|
La tasa de crecimiento es nula durante los primeros dos meses, y luego arranca y va creciendo junto con la población. Ahora hagamos los cálculos que nos piden.
f'(4) = 106. e(4 - 2)
|
|
|
| |
|
|
| Aún en buenas condiciones ambientales las bacterias suelen presentar tres fases de crecimiento: lag, exponencial y de estacionamiento. La última arranca cuando se empiezan a agotar los nutrientes. |
|
|
| |
|
|
| DESAFIO: Si en el período [0 ; 4] hubiese crecido a velocidad constante, ¿cuánto valdría esa velocidad? |
|
 |
| |
|
| |
|
| Algunos derechos reservados.
Se permite su reproducción citando la fuente. Última actualización mar-16. Buenos Aires, Argentina. |
|
|
| | |
|
|

