 |
NO ME SALEN
(EJERCICIOS RESUELTOS Y APUNTES TEÓRICOS DE FÍSICA)
Funciones derivadas
|
|

|
| |
NMS a2.03* - Al nacer un bebé normalmente perderá peso durante unos pocos días y después comenzará a ganarlo. Un modelo para el peso, P, de los bebés durante las primeras semanas de vida es:
P(t) = PN − 0,18 t + 0,015 t²
donde PN es el peso al nacer, el peso se mide en kgf y con t en días. Hallar el intervalo de disminución de peso.
|
| |
Una forma sencilla de resolver el ejercicio es graficar la función modelo, interpretar el gráfico y encontrar la respuesta. Otra manera es resolverlo analíticamente. Para ello buscamos la derivada de la función, P'(t):
|
|
|
P(t) = PN − 0,18 t + 0,015 t²
P'(t) = − 0,18 + 0,030 t
El peso dejará de disminuir y comenzará a aumentar (o sea, llegará su mínimo) cuando su derivada valga cero. P'(tm) = 0. A ese instante lo llamaremos tm. |
 |
|
|
|
0 = − 0,18 + 0,030 tm
Lo despejamos y calculamos:
tm = 0,18 / 0,030
tm = 6
De modo que el período de disminución, Δtdism, será: |
|
|
|
|
|
Y ya que estamos, grafiquemos la función modelo, interpretemos y verifiquemos el resultado. |
|
|
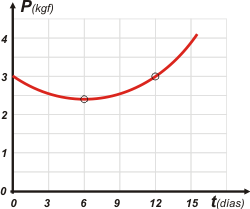 |
En rojo tenés la función del modelo, al que seguramente arribaron con mucha estadíastica y métodos matemáticos. Lo adapté a un peso en el nacimiento de 3 kgf, pero ya sabés que para otro peso al nacimiento (normal) basta con desplazar la curva hacia arriba o abajo.
Fijate que tal como habíamos predicho el peso alcanza su mínimo a los 6 días. Luego empieza a aumentar y recupera el peso inicial en el día 12. |
|
|
|
|
|
|
| *Adaptado de: Guía de Derivadas, Ignacio Trujillo Silva. (Disponible en la web). |
|
|
|
| DESAFIO: ¿Cuánto vale la pérdida de peso normal? |
|
 |
| |
|
| |
|
| Algunos derechos reservados.
Se permite su reproducción citando la fuente. Última actualización may-16. Buenos Aires, Argentina. |
|
|
| | |
|
|

