 |
NO ME SALEN
(EJERCICIOS RESUELTOS Y APUNTES TEÓRICOS DE FÍSICA)
Funciones derivadas
|
|

|
| |
NMS a2.01 - Hallar el valor de x para el cual la inclinación de la gráfica de la función
y = 0,5 x² − 2x − 1
vale 30 grados.
|
| |
| Bien. Sencillo y aleccionador ejercicio. Voy a arrancar por el gráfico para que te hagas bien la idea de lo que estamos buscando. |
|
|
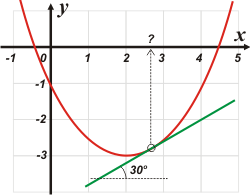 |
Ahí tenés en rojo la parábola (ya habías anticipado que se trataba de una parábola) que representa nuestra función:
y = 0,5 x² − 2x − 1
Como toda parábola, su inclinación va cambiando. En algún punto (eso es justamente lo que tenemos que averiguar) su inclinación vale 30°. Ese será el punto de tangencia con una recta inclinada 30° (representada en verde). |
|
|
|
Las inclinaciones de una curva que representa una función las describe la derivada de la función. De modo que buscamos la derivada.
y = 0,5 x² − 2x − 1
y' = x − 2
Y ahora nos formulamos la siguiente pregunta; ¿en qué valor de x la derivada representa una inclinación de 30°? Muy sencillo: las inclinaciones (o sea las pendientes) se representan con la tangente, al menos ése es el modo en que las representan las derivadas. Y:
tg 30° = 0,577
De modo que volvemos la derivada...
y'(30°) = x(30°) − 2
0,577 = x(30°) − 2
De ahí despejamos y calculamos ese x. |
|
|
|
|
|
| Pero lo más importante es que interpretes el resultado. Mirá este gráfico. |
|
|
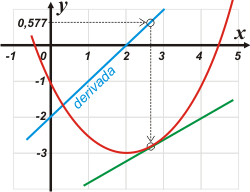 |
En rojo tenés la misma función de antes... y en azul aparece la función derivada.
Fijate que la recta que representa la función derivada ¡nada tiene que ver con la recta tangente que te representé en el gráfico anterior! ¡Son cosas diferentes!
Lo que hicimos fue buscar en esa recta de la derivada con qué valor de x la ordenada valía 0,577, o sea, tg 30°. |
|
|
|
En el ejercicio siguiente vamos a repetir esta misma lección, pero va a ser más fuerte, porque la función derivada no va a ser lineal. |
|
|
| DESAFIO: ¿En qué posición la inclinación vale 45°? |
|
 |
| |
|
| |
|
| Algunos derechos reservados.
Se permite su reproducción citando la fuente. Última actualización may-16. Buenos Aires, Argentina. |
|
|
| | |
|
|

