 |
NO ME SALEN
(EJERCICIOS RESUELTOS Y APUNTES TEÓRICOS DE FÍSICA)
Funciones - Trigonometría
|
|

|
| TEOREMA DEL SENO - Demostración |
| |
El teorema del seno estan sencillo y fácil de memorizar que no tenerlo a mano es un despropósito. Se trata de un teorema aplicable a cualquier triángulo. |
| |
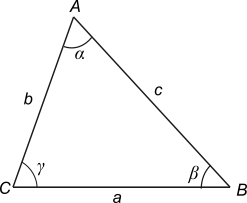 |
Supongamos un triángulo cualquiera de vértices:
A, B y C.
Los ángulos correspondientes a cada vértice son:
α, β y γ.
Y los lados (opuestos a cada vértice):
a, b y c.
|
|
|
|
| El teorema dice: |
|
|
| |
| |
sen α |
= |
sen β |
= |
sen γ |
|
|
|
|
| a |
b |
c |
|
|
|
|
|
DEMOSTRACIÖN: La demostración original parte de un triángulo inscripto en una circunferencia y las relaciones de los ángulos con el radio de esa circunferencia. Acá te presento una alternativa que no requiere conocimiento de circunferencias y se basa exclusivamente en la función seno (opuesto sobre hipotenusa, triángulos rectángulos). |
|
|
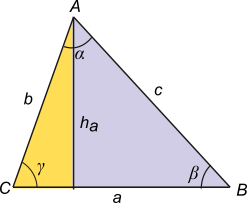 |
Tracemos una de las alturas del triángulo, ha. Entonces el triángulo original queda dividido en dos triángulos rectángulos (no te olvides que las alturas son ortogonales al lado correspondiente).
Entonces, en el triángulo amarillo:
sen γ = ha / b
Y en el triángulo violeta: sen β = ha / c
|
|
|
|
| De ambas expresiones despejamos ha y las igualamos. Nos queda: |
|
|
|
|
|
| Supongo que ya te diste cuenta por dónde viene la mano. Ahora trazamos otra altura cualquiera, por ejemplo la del lado c. |
|
|
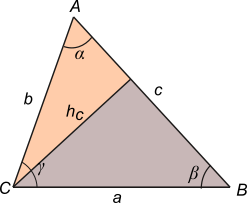 |
Y el triángulo original queda dividido en dos nuevos triángulos rectángulos.
Entonces, en el triángulo beige:
sen α = hc / b
Y en el triángulo morado:
sen β = hc / a
Y volvemos a hacer lo mismo de antes, despejamos hc de ambas e igualamos. |
|
|
|
|
|
|
El segundo miembro de ambas expresiones es el mismo. Luego, los tres miembros deben ser iguales, con lo que llegamos a nuestro teorema.
Una formulación literal podría ser ésta: en un triángulo cualquiera, la razón entre el seno de un ángulo y su lado opuesto es constante.
Tenés otra demostración más, y diferente, en el capítulo de vectores, acá. |
|
 |
| |
|
| |
|
| Algunos derechos reservados.
Se permite su reproducción citando la fuente. Última actualización may-21. Buenos Aires, Argentina. |
|
|
| | |
|
|

