 |
NO ME SALEN
(APUNTES TEÓRICOS Y EJERCICIOS DE BIOFÍSICA DEL CBC)
CALOR Y TERMODINÁMICA
|
|

|
 |
 |
EM - Problema 17 -
Un mol de gas ideal evoluciona en forma reversible desde una presión de 1,2 atm y un
volumen de 5 litros hasta una presión de 4 atm y un volumen de 1,5 litros. En esa evolución
la variación de energía interna del gas (ΔU) y la variación de entropía del gas (ΔS) valen
a) ΔU = 0, ΔS = 0 b) ΔU = 0, ΔS > 0 c) ΔU = 0, ΔS < 0
d) ΔU > 0, ΔS = 0 e) ΔU< 0, ΔS < 0 f) ΔU < 0, ΔS > 0
|
|
| |
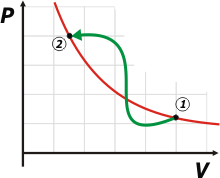
Observá este gráfico; está hecho en escala. Llamé 1 al estado inicial del gas ideal, con 1,2 atm y 5 lt; y 2 al estado final, con 4 atm y 1,5 lt. La gráfica verde representa una evolución cualquiera de las infinitas posibles, lo único que te indica el hecho de que esté dibujada es que la evolución es reversible.
La curva roja es una isoterma, o sea: un conjunto infinito de estados posibles todos con diferente presión y diferente volumen, pero todos con la misma temperatura. De ahí su nombre. La dibujé sólo como un elemento auxiliar para resaltar el concepto que sigue.
¿Cómo supe que los estados 1 y 2 tienen la misma temperatura, o sea, se hallan sobre la misma isoterma? No se podía saber a priori, pero yo hice las cuentas y me da eso. La relación entre dos estados predice que: |
|
|
 |
|
Si reemplazás los valores de presión y volumen de ambos estados, vas a encontrar que las temperaturas T1 y T2 son iguales, por eso las representé así.
En este ejercicio, la cuestión de la temperatura es fundamental, ya que si la variación de temperatura es nula, también lo es la diferencia de energía interna, ya que en los gases ideales la energía interna depende exclusivamente de la temperatura.
ΔT = 0 entonces ΔU = 0
|
|
|
|
Con eso respondemos la primera parte de la pregunta del ejercicio. Para la segunda vamos a aprovechar lo que ya sabemos, y buscar ayuda en el primer principio de la termodinámica.
Q = ΔU + L
Como la variación de energía interna valía cero, tenemos:
Q = L
Ahora bien, en la evolución del gas, desde el estado 1 al 2, hay una reducción de volumen (sea cual sea el camino de la evolución, el volumen final es menor que el inicial), de modo que el trabajo es negativo. Y por la igualdad que acabo de escribir
L < 0 entonces Q < 0
Por último, acordate que la variación de entropía es la suma integral de todos los pequeños intercambios de calor, divididos por la temperatura absoluta a la que ocurrió ese intercambio. En símbolos: |
|
|
|
|
|
Ese denominador es positivo siempre, ya que no existen temperaturas absolutas negativas. De modo que el signo del cociente depende exclusivamente de la suma de los intercambios de calor, y eso ya vimos que era negativo. Para hacértela corta:
Q < 0 entonces ΔS < 0
En definitiva: |
|
|
ΔU = 0, ΔS < 0 respuesta c) |
|
|
|
| |
|
|
Desafío: Necesito una respuesta categórica para esta pregunta: ¿puede saberse cuánto vale esa disminución de entropía? Si es sí: ¿cuánto vale? Si es no: ¿por qué? |
|
 |
| |
|
| Algunos derechos reservados.
Se permite su reproducción citando la fuente. Última actualización ene-08. Buenos Aires, Argentina. |
|
|
| | |
|
|

