NO ME SALEN
(APUNTES TEÓRICOS Y EJERCICIOS DE BIOFÍSICA DEL CBC)
CALOR Y TERMODINÁMICA
|
|

|
| |
 |
EM - Problema 8.
Sean dos recipientes cúbicos A y B conteniendo hielo. Las paredes son adiabáticas, salvo la
superior que está expuesta al aire. Los cubos de hielo están a una temperatura inicial de
0ºC y la arista del cubo A es la mitad de la del cubo B. En el mismo lapso en que el cubo A
se funde totalmente, la masa de B que se funde es: |
| |
a) toda;
b) la cuarta parte de su masa inicial;
c) la mitad de su masa inicial;
d) la octava parte de su masa inicial;
e) la décima parte de su masa inicial;
f) la tercera parte de su masa inicial.
|
|
| |
Muy bien. Imagino que ya lo intentaste... no es sencillo, y posee múltiples abordajes diferentes. Yo te voy a hacer uno y voy a ir marcando todos los escollos en los que -tal vez- te hayas trabado. |
|
|
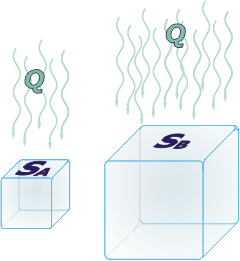 |
Acá te representé los cubitos de hielo, en escala; y no los recipientes, pero es lo mismo: el calor sólo entra por la cara superior.
Supongo que te queda claro que entra más calor al cubito grande, porque la cara superior es más grande. Al mismo tiempo necesita mucho más calor para fundirse, porque tiene mucha más masa de hielo para fundir.
Todo el problema gira en torno a estas relaciones de tamaño entre los dos cubos, así que vamos a empezar por ahí: por poner en claro esas cuestiones de tipo geométrico. Son relaciones de las que vos tenés que darte cuenta sin ayuda: no esperes encontrar un capítulo de un libro de física que te lo enseñe. |
|
|
|
| Acá te hice nuevamente una representación gráfica de los cubitos (a escala): el A metido repetidas veces dentro del B. |
|
|
 |
Para el cubito B, el hecho de poseer una arista el doble de largo que la del cubito A, hace que tenga un área 4 veces mayor, y un volumen 8 veces mayor. En ecuaciones:
SB = 4 SA
VB = 8 VA
como la densidad del hielo es la misma en ambos cubos, la última queda:
mB = 8 mA
|
|
|
|
| Tal vez te diste cuenta de que las relaciones de arista, de área 2 de volumen, siguen la secuencia: lineal, cuadrática y cúbica. Fijate: 2¹= 2; 2²= 4; 2³= 8. Fue Galileo Galilei el primero en darse cuenta de que había muchos fenómenos naturales que obedecían esta relación, y la llamó ley cuadrático-cúbica. En biología se trata de una ley fundamental. |
|
|
|
Ahora sí, podemos comenzar con el problema. Vamos a usar la Ley de Fourier para describir el ingreso de calor a los cubos: |
|
|
|
|
|
Y la ley de la calorimetría para cambios de estado.
Q = m . L
La diferencia de temperatura entre el hielo y el aire, ΔT, no sabemos cuánto vale, pero sabemos que vale lo mismo en ambos casos. Algo parecido ocurre con la longitud que tiene que atravesar el calor, Δx (en realidad se trata de una diferencia de espesor de una película de agua líquida que el autor del problema decidió despreciar). El calor latente de fusión del hielo, L, es el mismo -lógicamente- para ambos cubitos.
La cantidad de calor necesaria para derretir todo el cubo A estará dada por:
QA = mA . L
El intervalo de tiempo necesario para ese derretimiento, ΔtA, se lo consultamos a la ecuación de Fourier (fijate: ya te la presento con el intervalo despejado): |
|
|
| |
ΔtA = |
– QA . Δx |
|
| k . SA . ΔT |
|
|
|
| Las combino para que el intervalo quede expresado en función de la masa del cubo A. |
|
|
| |
ΔtA = |
– mA . L . Δx |
|
| k . SA . ΔT |
|
[1] |
|
|
| Ahora vamos con ese intervalo al cubo B. Reemplacemos el intervalo ΔtA (que tardó el derretimiento del cubo chico) en la ecuación de Fourier que describe el ingreso de calor en el cubo B: |
|
|
| |
QBA |
= |
– k . SB . ΔT |
|
|
| ΔtA |
Δx |
|
|
|
Esta es la Ley de Fourier aplicada al cuerpo B y donde QBA es la cantidad de calor que entró en el cubo grande durante la misma cantidad de tiempo en que el cubo chicho se derritió totalmente, ΔtA.
Podés mirarlo así (simplemente paso de miembro ΔtA). |
|
|
| |
QBA = |
– k . SB . ΔT . ΔtA |
|
| Δx |
|
|
|
| En ella reemplazo ΔtA por su igual tal como aparece en la Ley de Fourier aplicada al cuerpo A (ecuación [1]). |
|
|
| |
QBA = |
k . SB . ΔT . mA . L . Δx |
|
| k . SA . ΔT . Δx |
|
|
|
Cancelo los factores iguales. Y acordate que SB = 4 SA.
QBA = 4 . mA . L
Tenés que entender que esa cantidad de calor es mayor que la que entró en el cubo chico... porque la "ventana" del cubo grande es más grande... le entra más calor.
Para saber qué fracción del cubo B se derritió me basta con dividir el calor que le entró, QBA, por el calor necesario para derretirlo totalmente, QB; siendo esa cantidad de calor:
QB = mB . L
Hago el cociente: |
|
|
| |
QBA |
= |
4 . mA . L |
|
|
| QB |
mB . L |
|
|
|
|
|
|
| Finalmente utilizo las equivalencias geométricas entre los cubos (mB = 8 mA): |
|
|
| |
|
|
| |
|
|
|
c) la mitad de su masa inicial. |
|
|
|
Discusión: cualquier profesor de física, o cualquier ingeniero o físico, habrían leído las opciones y acertado de una. Ya internalizaron que la trasmisión de calor tiene que ver con el área (el cubo grande es cuatro veces mayor) y que el derretimiento tiene que ver con la masa (el cubo grande es ocho veces mayor), luego, con un razonamiento de 6 microsegundos se habrían dado cuenta de que en el mismo tiempo que se derrite todo el cubo chico se derrite medio cubo grande. tal vez yo tendría que haberte resuelto el ejercicio aplicando esos razonamientos (no en 6 microsegundos, claro está). Pero preferí resolverlo formalizado totalmente... y aguardar que vos vayas internalizando los conceptos de a poco. No sé si hice bien.
Desafío:
¿Cuánto se habría derretido si la arista de B fuera tres veces más grande que la de A? Animate a resolverlo primero mentalmente, después algebraicamente. |
|
 |
| Algunos derechos reservados.
Se permite su reproducción citando la fuente. No me salen es la única fuente de ejercicios resueltos producido con normas internacionales de calidad y asepsia. Última actualización mar-08. Buenos Aires, Argentina. |
|
|
|

