NO ME SALEN
(APUNTES TEÓRICOS Y EJERCICIOS DE BIOFÍSICA DEL CBC)
CALOR Y TERMODINÁMICA
|
|

|
| |
 |
EM - Problema 6 -
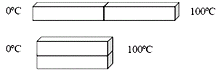
Dos barras rectangulares idénticas
están unidas como se muestra en la
figura superior, de modo que cuando
las temperaturas son las indicadas, en
régimen estacionario, se transmiten a
través de ellas 10 calorías por minuto.
¿Cuál sería la potencia transmitida si estuvieran unidas como se muestra en la figura
inferior?
En ambas situaciones el sistema está aislado lateralmente. |
a) 20 calorías por minuto
b) 10 calorías por minuto
c) 40 calorías por minuto
d) cero
e) 2,5 calorías por minuto
f) calorías por minuto |
 |
|
| |
Se trata de un ejercicio bastante sencillo, de aplicación de la Ley de Fourier, que describe la conducción del calor. |
|
|
|
|
|
en el que tenés dos situaciones, de algún modo relacionadas entre sí. Llamemos A a la situación inicial y B a la situación posterior. La potencia de la conducción en la situación A vale Q/Δt = 10 cal/min.
Te hice un esquema porque encontré varios estudiantes que no pudieron interpretar correctamente el fenómeno. Es cierto que el enunciado no es del todo explícito... (¡los físicos!). |
|
|
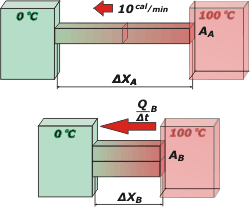 |
Ahí tenemos las dos situaciones: está claro que
AB = 2 AA
y que
ΔxB = ½ ΔxA
¿Estamos? Además, la diferencia de temperaturas es la misma en ambas situaciones; y la constante de conductividad térmica también, porque sólo depende del material y no de su forma. Entonces... |
|
|
|
| |
QA |
= |
– k . AA . ΔT |
= 10 cal/min |
|
|
| Δt |
ΔxA |
|
|
|
| Y en la situación B |
|
|
| |
QB |
= |
– k . AB . ΔT |
|
|
|
| Δt |
ΔxB |
|
|
|
| Ahora, en esta última, reemplazo el área y la longitud por sus iguales... ( AB = 2 AA y ΔxB = ½ ΔxA ). |
|
|
| |
QB |
= |
– k . (2 AA) . ΔT |
|
|
|
| Δt |
(½ ΔxA) |
|
|
|
| Saco esos factores afuera del cociente (el orden de los factores no altera el producto). |
|
|
| |
QB |
= 4 . |
( |
– k . AA . ΔT |
) |
|
|
| Δt |
ΔxA |
|
|
|
| Lo que quedó dentro del paréntesis no es otra cosa que la potencia en el caso A. |
|
|
|
|
|
|
|
|
| |
QB |
= 40 cal/min |
respuesta c) |
|
| Δt |
|
|
|
|
|
| |
|
|
Desafío:
Ahora sin hacer ninguna cuenta, suponete que la primera barra la partimos en 3 segmentos iguales y los ponemos uno al lado del otro conectando las fuentes... ¿cuánto valdrá la potencia de la conducción? |
|
 |
| |
|
Algunos derechos reservados.
Se permite su reproducción citando la fuente. Se recomienda fervientemente no meter la mano en agua hirviendo. Última actualización nov-07. Buenos Aires, Argentina. |
|
|
| | |
|
|

