NO ME SALEN
(APUNTES TEÓRICOS Y EJERCICIOS DE BIOFÍSICA DEL CBC)
CALOR Y TERMODINÁMICA
|
|

|
| |
 |
EM - Problema 5 -
Un iglú tiene forma semiesférica, 2 metros de radio interno, y está construido con bloques
de hielo de 40 cm de espesor. Si la temperatura de la cara interior de la pared de la
vivienda es de 0ºC y la de la cara exterior, –40 ºC, calcule cuánto calor se transmite por
conducción a través de las paredes en una hora (khielo = 0,0004 kcal/ºC m s). Observe que
la superficie a través de la cual fluye el calor no es constante, como lo es en el caso de
una varilla o una pared plana. No obstante, para las condiciones del problema, es una
buena aproximación considerarla constante y tomar como radio de la misma el promedio de
los radios de las caras interna y externa. |
a) 4.380 kcal b) 8.734 kcal c) 2.189 kcal
d) 1,2 kcal e) 43,8 kcal f) 4,18 kcal |
|
| |
Se trata de un ejercicio bastante sencillo, de aplicación de la Ley de Fourier, que describe la conducción del calor:
|
|
|
|
|
|
No te niego que el ejercicio tenga algunas dificultades, pero no me parece que sean de naturaleza física. Por ejemplo: ¿cuál es el área que tiene el calor para retirarse del iglú?: toda su semiesférica pared. Se trata, entonces, de un área esférica. ¿Te acordás cómo hacer para hallar el área de una esfera conociendo su radio? Seguro que no, pero no te preocupes: eso le pasa a la mayoría de las personas a menos que sean esquimales. Te lo digo yo (se trata del tipo de información que suele acompañar el enunciado como dato adicional; esta vez no).
A = 4 π R²
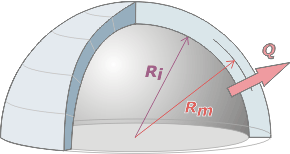
Como nuestro iglú es la mitad de una esfera tendremos que dividir esa área por dos. Pero hay otra cuestión que resolver: ¿qué radio vamos a utilizar para el cálculo del área? La pregunta es pertinente porque, como te darás cuenta, el área interior es menor que el área exterior... El enunciado sugiere que tomemos el radio medio y me parece que le vamos a hacer caso. Como la pared tiene 40 cm de ancho, el radio medio medirá: Rm = 2,2 m. |
|
|
 |
De modo que el área resulta igual a
A = 2 π (2,2 m)²
A = 30,4 m²
Fijate que en el esquemita que hice indiqué la salida de calor con una única flecha: está claro que sale por todo lo ancho de la pared, y atravesando una longitud de hielo de Δx = 0,4 m. |
|
|
|
Calculemos, entonces, la potencia con la que el calor huye del iglú:
Q/Δt = – k . A . ΔT / Δx
La conductividad térmica del hielo, k, es un dato del enunciado*: 0,0004 kcal/ºC m s
Q/Δt = – 0,0004 (kcal/ºC m s) . 30,4 m². (-40ºC) / 0,4 m
Q/Δt = 1,216 kcal/s
Si querés saber cuánto calor sale en una hora, podés multiplicar la potencia anterior por la cantidad de segundos que hay en una hora, 3.600 s:
Q = 1,216 (kcal/s) . 3.600 s =
|
|
|
| |
Q = 4.380 kcal respuesta a) |
|
|
|
 |
Me gustaría que analices este resultado. La energía calórica de la leña es más o menos 4.000 kcal por kilogramo, eso quiere decir que quemando apenas un kilo de leña por hora evitás congelarte dentro de un iglú en un clima de -40ºC. Sorprendente, ¿no?
*El dato consignado es menor que el verdadero.
|
|
Desafío:
¿A que no encontrás un iglú igual a éste? |
|
| |
|
| Algunos derechos reservados.
Se permite su reproducción citando la fuente. Está absolutamente desaconsejado revelarle a un esquimal que su esposa nos hace ojitos. Última actualización nov-07. Buenos Aires, Argentina. |
|
|
| |
|
|
|

