home  | más sobre termo | otros temas de Física | lecciones del maestro Ciruela | tonterías |  @ 
   NO ME SALEN
   (APUNTES TEÓRICOS Y EJERCICIOS DE BIOFÍSICA DEL CBC)
   CALOR Y TERMODINÁMICA

 

nomesalen

 
EM - Problema 4 - Una varilla metálica, cuyos extremos están uno a 250°C y el otro a 40°C, conduce 75,4 cal/s. Si su longitud y su diámetro se reducen a la mitad, y se colocan sus extremos a las mismas temperaturas que antes, la varilla conducirá (en cal/s):
    a) 75,4     b) 7,5     c) 18,9     d) 754     e) 150,8     f) 37,7
 

No problem... Se trata de un sencillo ejercicio de conducción del calor, fenómeno que se describe con la Ley de Fourier:

    
  Q = – k . A . ΔT
Δt Δx
   

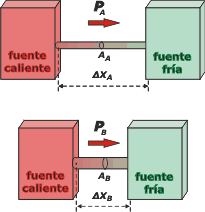
Al flujo de conducción (Q/Δt) lo voy a llamar P (por potencia) para agilizar la notación. Y llamemos A a la primer varilla (que hay que suponer cilíndrica ya que nos hablan de diámetro) y B a la segunda. Entonces tenemos que:

PA = 75,4 cal/s

Y que PB es nuestra incógnita.

La principal dificultad de este ejercicio es de tipo geométrica. Según el enunciado:

   

ΔxB = 0,5 ΔxA

dB = 0,5 dA

Donde dB y dA son los diámetros de las dos barras. Pero a la ecuación de Fourier no le importan los diámetros sino las áreas, las secciones. Por suerte hay una relación inmediata entre diámetro y área: A = π d²/4, de modo que si elevamos la última ecuación al cuadrado,

(dB)² = (0,5 dA)²

dB² = 0,25 dA²
   

Y la multiplicamos por π/4...

π dB² /4 = 0,25 . π dA² /4

llegamos a la conclusión de que el área de la segunda barra es la cuarta parte del área de la primera:

AB = 0,25 AA

Tené presente estas relaciones que las vamos a necesitar. Ahora expresamos las conducciones para ambos casos:

PA= – k AA ΔT / ΔxA = 75,4 cal/s

PB = – k AB ΔT / ΔxB

En esta última puedo usar las equivalencias geométricas que planteamos al principio:

PB = – k (0,25 AA) ΔT / (0,5 ΔxA)

PB = – 0,5 k AA ΔT / ΔxA

Ahí apareció una expresión que contiene a PA:

PB = 0,5 . PA

PB = 0,5 . 75,4 cal/s

PB = 37,7 cal/s

En la notación corriente:

    

 

            QB /Δt = 37,7 cal/s  
   

Viste, no fue necesario utilizar los valores de las temperaturas; sólo importaba el hecho de que la diferencia de temperatura entre los extremos era la misma en ambos casos, de modo que ni siquiera le puse subíndice a la diferencia.

   

Desafío: ¿Cuánto valdrá la conducción de las dos varillas juntas? ¿Y una a continuación de la otra?

  
   
Algunos derechos reservados. Se permite su reproducción citando la fuente. Lema Cuarto de la Calorimetría: si tu novia está recaliente no te hagas el tonto. Última actualización mar-08. Buenos Aires, Argentina.