NO ME SALEN
(APUNTES TEÓRICOS Y EJERCICIOS DE BIOFÍSICA DEL CBC)
CALOR Y TERMODINÁMICA
|
|

|
| |
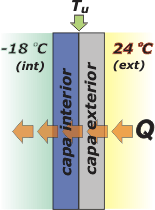
Adicional No me salen 45* El interior de un freezer que se encuentra a –18°C está separado del exterior, que está a 24°C, por dos capas de material aislante del calor del mismo espesor. La capa interna, en contacto con el interior, tiene una conductividad térmica que es la sexta parte de la conductividad térmica de la capa externa, en contacto con el exterior. Si se alcanzó el estado estacionario, la temperatura de la unión entre ambas capas es: a) 3°C b) -12°C c) -4°C d) 18°C e) 8°C f) 13°C |
|
| |
| Este ejercicio perteneció al examen final de Biofísica tomado el 23 de junio de 2010. Para ver el tema completo hacé clic acá. |
|
|
|
OK, bastante sencillo. Con una mirada experta se puede contestar si hacer ninguna cuenta. Pero hagámosnos los giles y resolvamos el ejercicio como si fuésemos principiantes. Mirando las opciones que nos dan es obvio que hay que conocer la temperatura intermedia, en el contacto entre la capa interna (mala conductora) y la externa (buena conductora).
Todo el calor que atraviesa la capa externa debe atravesar, también, la interna, de modo que: |
|
|
|
|
|
| Esos pasajes de calor son descriptos por la ley de Fourier: |
|
|
| |
– kext . A . (Tu – 24°C) |
= |
– kint . A . (–18°C – Tu) |
|
|
| Δx |
Δx |
|
|
|
| Donde Tu es la temperatura de unión, que queremos conocer. Acá tenés un esquema que aclara los puntos: |
|
|
La áreas, A, y los espesores, Δx, son los mismos para las dos capas. De modo que la igualdad anterior puede simplificarse de este modo:
kext . (Tu – 24°C) = kint . (–18°C – Tu)
Pero el enunciado también agrega una relación entre las conductividades de los dos materiales: kext = 6 kint. Si metemos eso en la igualdad anterior, tendremos:
6 kint . (Tu – 24°C) = kint . (–18°C – Tu) |
|
|
|
|
6 . (Tu – 24°C) = (–18°C – Tu)
6 Tu – 144°C = –18°C – Tu
7 . Tu = 126°C
|
|
|
|
|
|
Pero ya te lo advertí... era predecible. Un ejercicio correctamente diseñado para un examen -como éste- le permite al estudiante que conoce conceptualmente el tema resolverlo sin hacer ninguna cuenta. Fijate:
La temperatura intermedia tiene que ser un valor comprendido entre las temperaturas externa e interna, eso lo cumplen todas las opciones. Si las conductividades de los materiales fuesen iguales la temperatura intermedia tendría que ser justo el promedio entre la exterior y la interior, o sea, 3°C, pero no lo son, de modo que esa opción podemos descartarla.
Como el material exterior es mejor conductor que el material interior la temperatura de contacto debe ser más próxima a la temperatura exterior que a la interior, o sea que podemos descartar las temperaturas –4°C y –12°C.
Finalmente, como no son conductividades parecidas, sino muy diferentes (una es 6 veces mayor que la otra) la temperatura intermedia debe ser muy próxima a la interior, o sea, nos quedamos con la correcta.
De hecho, si te fijás las diferencias de temperatura dentro de cada material, una diferencia es 6 veces más grande que la otra. |
|
|
Desafío:
¿Cuál sería la temperatura en la unión si se invirtiese el orden de las capas (figura entre las opciones)? ¿Te animás a resolverlo sin hacer cuentas? |
|
 |
| |
| |
|
| Algunos derechos reservados.
Se permite su reproducción citando la fuente. Agradezco a Karen Molinatti por el envío de una errata. Principio Fundamental de la Termodinámica: si tu novio está recaliente, siempre hay un modo de solucionarlo. Última actualización jul-14. Buenos Aires, Argentina. |
|
|
| | |
|
|

