NO ME SALEN
(APUNTES TEÓRICOS Y EJERCICIOS DE BIOFÍSICA DEL CBC)
CALOR Y TERMODINÁMICA
|
|

|
| |
Adicional 36*) Suponiendo que la cantidad de carbón necesaria para mantener la caldera de una máquina de tren a 250 ºC no depende de la temperatura exterior, sabiendo que las temperaturas medias diurna y nocturna en el Sahara son de 50 ºC y -10 ºC, y suponiendo que la máquina es ideal, ¿qué reducción habría en el presupuesto de carbón de los ferrocarriles del Desierto S. A., si los servicios fueran nocturnos y no diurnos, como es habitual? |
|
| |
 |
|
|
La única modificación que le hice al enunciado de este bonito ejercicio es la siguiente: en lugar de decir máquina ideal, el original decía máquina de Carnot (un asunto que no se desarrolla en No me salen pero que, para el caso, deben entenderse como expresiones equivalentes.
Si te acordás que los asuntos de máquinas térmicas deben manejarse con temperaturas absolutas y los datos aportados por el enunciado vienen en grados celsius, esquematicemos los funcionamientos de la máquina en las dos situaciones: |
|
|
funcionamiento
diurno |
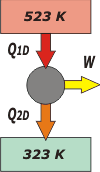
En el funcionamiento diurno las temperaturas de trabajo son 523 K la caldera y 323 K el aire cálido del desierto en el que se vuelcan los gases que salen de la máquina (por las chimeneas de la locomotora) que se llevan el calor desperdiciado.
Q1D es el calor que debe entregar la caldera funcionando de día. Q2D es el calor desperdiciado durante el funcionamiento diurno. W es el trabajo que hace la máquina que, suponiendo que debe tirar del mismo tren y con la misma cantidad de pasajeros, será el mismo ya viaje de día como de noche.
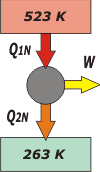
En el funcionamiento nocturno las temperaturas son: 523 K y 263 K. |
 |
|
|
|
funcionamiento
nocturno |
Y los calores intercambiados durante la noche: Q1N y Q2N.
Como se trata de una máquina que funciona idealmente, el rendimiento
η = 1 – (Q2/Q1)
es igual a:
η = 1 – (T2/T1)
De modo que los rendimientos funcionando de día, ηD, y de noche, ηN, valdrán: |
 |
|
|
|
ηD = 1 – (323 K/523 K)
ηD = 0,38
ηN = 1 – (263 K/523 K)
ηN = 0,50
Como vemos, el funcionamiento nocturno es mucho más rendidor. Pero la pregunta del enunciado es ¿cuánto valdrá la reducción de presupuesto, o sea, cuánto menos combustible habrá que comprar. O sea: cuánto vale Q1N en función de Q1D.
De la propia definición de rendimiento (beneficio sobre inversión),
η = W /Q1
Y recordando que tanto de día como de noche la máquina tiene que realizar el mismo trabajo, podemos escribir:
ηN Q1N = ηD Q1D
De donde:
Q1N = (ηD /ηN) Q1D
Q1N = (0,38 / 0,50) Q1D
Q1N = 0,76 Q1D
Con el 76% de la cantidad de carbón que se compra para funcionar de día, podría hacer los mismos viajes, si los hiciese de noche. |
|
|
de noche funcionaría con una reducción del 24% |
|
|
|
| Eso sí... no habrá que olvidarse la bufanda. |
|
|
| |
|
|
* Tomado y adaptado de Física para las Ciencias de la Vida, Jou, Llebot y Pérez García, Ed. Mc Graw Hill, p. 206. |
|
|
|
| |
|
|
Desafío:
Además de más económico, ¿cuánto más ecológico es el andar nocturno? O sea: ¿cuál es la relación entre desperdicios? |
|
 |
| |
|
| Algunos derechos reservados.
Se permite su reproducción citando la fuente. Cuando te acalores quítate la ropa, pero con cierto pudor. Última actualización oct-13. Buenos Aires, Argentina. |
|
|
| | |
|
|

